Quadrik in affiner Normalform. Ursprung ihres Koordinatensystems und die Hauptachsentransformation explizit angeben.

Question

Ich hab folgenden Quadrik gegeben
3x1²-2x1x2+3x2²+6\( \sqrt{2} \) x1-2\( \sqrt{2} \) x2-2


und habe dazu auch schon die affine Normalform bestimmt jetzt muss ich noch den Ursprung des Koordinatensystems  und die Transformation explizit angeben und die Quadrik im Standardkoordinatensystem skizzieren
Leider weiß ich nicht genau wie das funktioniert  bzw. wo man das ablesen kann

Schon mal Vielen Dank

Nachtrag: Aufgabe war nämlich die Quadrik in affine Normalform zu bringen und dann als zweite Aufgabe: Geben sie den Ursprung ihres Koordinatensystems und die Transformation explizit an.

Comments

Was hast du denn raus für die Normalform ?

---

1.

Ursprung des Koordinatensystems 

?

Ist das nicht immer der Punkt O(0|0) ?

2. Wie ist deine Überschrift genau gemeint?

---

aber ja nicht nach einer Hauptachsentransformation da verschiebt man doch dass Koordinatensystem um die Quadrik leichter zu beschreiben, falls ich das richtig verstanden habe

---

Ah ja, dann war das sozusagen die

Vorbereitung der HA-Transformation.

Der Mittelpunkt im xy-Koordinatensystem ist

ja dann auch nicht  (-1 ; -1 ) sondern ( -√2 ; 0 ) .

---

Also ich bin mir da überhaupt nicht sicher, die Aufgabe war nämlich die Quadrik in affine Normalform zu bringen und dann als zweite Aufgabe: Geben sie den Ursprung ihres Koordinantensystems und die Transformation explizit an, deswegen weiß ich nicht so genau was gemacht werden muss

---

Geben sie den Ursprung ihres Koordinatensystems und die Transformation explizit an.

Wegen "ihres" müsste das wohl M( -√2 ; 0 ) sein.

---

Wo bekommt man denn den Wert her, also des Mittelpunktes?

---

Transformationsmatrix * (-1 ; -1) ^T

Answer 1

Du hast wohl noch das " =0 " vergessen.

Nach Hauptachsentransformation komme ich auf die Gleichung

(im neuen ab-Koordinatensystem)

(a+1)^2 / 4  + (b+1)^2 / 2 = 1

Also ist der Mittelpunkt bei ( -1 ; -1 ) und die

Halbachsen werden durch die Vektoren

( √2 ; √2 )^T und ( 0,5*√2 ; -0,5*√2 ) gegeben.

Damit kannst du die Ellipse doch schon zeichnen durch die

Punkte (0; √2 ) , ( -1-√2 ; 1) , (-2√2 ; -√2 ) und (1-√2 ; -1) .

Das sind dann die Scheitel.

siehe auch:

https://www.wolframalpha.com/input/?i=3*x%5E2-2*x*y%2B3*y%5E2%2B6*sqrt%282%29*x-2*sqrt%282%29*y-2%3D0

Comments

Stimmt das ''=0'' habe ich vergessen, vielen Dank

ich muss meine Rechnung nochmal durchgehen ich denke ich habe mich verrechnet

meine Form nach der quadratischen Ergänzung ist

4(y1-\( \frac{1}{2} \))²  + 2(y2+2)² -11

dann habe ich  substituiert mit z1=y1 - \( \frac{1}{2} \)

z2= y2+2

dann hab ich das ein wenig zsmgefasst um auf die Form die immer für Quadriken angegeben ist zu kommen

\( \frac{z1²}{\(sqrt{\frac{11}{4}})^2\) leider bekomme ich das gerade nicht hin 

ich meine z1^2/(sqrt(11/4))^2 + z2^2/(sqrt(11/2))^2 -1

das wäre meine Normalform

Den Mittelpunkt kann man anscheind jetzt einfach ablesen, das habe ich verstanden aber wie bekommt man die Halbachsen?

---

Die Halbachsen sind die Werte die im Nenner stehen

ohne das hoch 2.

Bei dir wären das sqrt(11/4) und (sqrt(11/2)

Ich hatte ja (a+1)2 / 4  + (b+1)2 / 2 = 1 ,

also Halbachsen 2 und √2.

Answer 2

Mal einen Versuch

https://www.geogebra.org/m/jybmgrce

3x² + 3y² - 2 x y + 6sqrt(2) x - 2sqrt(2) y = 2

Für exakte Rechnung müssen die wurzelbehafteten Werte direkt ins CAS geschrieben werden

==> (5) C:={3,3,-2,-2,6sqrt(2),-2sqrt(2)}

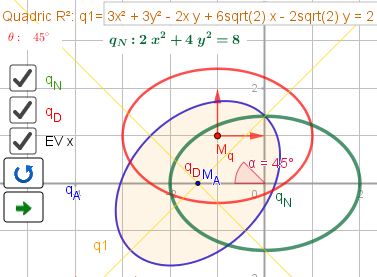
Transformation (22)

\(T \, :=  \,  \left\{ x = x - 1, y = y + 1, -6 \right\} \)

\(E \, :=  \,  \left\{ \frac{x^{2}}{a_o^{2}} + \frac{y^{2}}{b_o^{2}} = 1, a_o^{2} = 4, b_o^{2} = 2 \right\} \)

==>

\( \left\{ Achsenlängen, \left|a_o\right| = 2, \left|b_o\right| = \sqrt{2} \right\} \)

___

WEnn Du in dem Programm mit dem Vorzeichen beim Faktor 2 sqrt(2)  y spielst, dann hast Du die Achsen, die Dir vorschweben...