In einem Casino sollen gefälschte Würfel im Spiel sein, die mit 25% 6 würfeln, Casino prüft Würfel durch 100 Testwürfe zu prüfen. Wie Entscheidungsregel, damit die Wahrscheinlichkeit einen gefälschten Würfel durchzulassen kleiner als 5% ist? Und wie gross ist die Irrtums-WK mit der Regel?
Dein Ansatz war schon nicht schlecht. Du müsstest allerdings die WK von einem gefälschten Würfel nehmen, weil es darum geht ihn durchzulassen.
binomcdf(100, 0.25, k) < 0.05
Und genau. Du könntest jetzt für k eine Wertetabelle machen und denjenigen Wert der gerade unter 5% ist heraussuchen und das k notieren.
Weiter könntest du schauen ob dein Taschenrechner auch die inverse Binomialverteilung beherrscht. Damit könnte man dann auch das k ausrechnen.
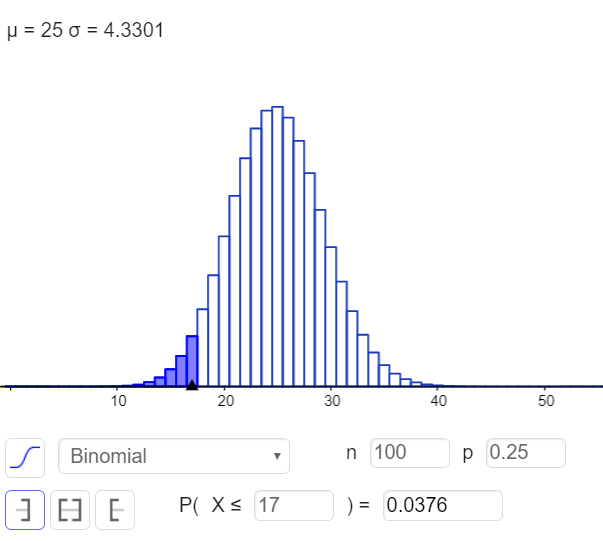
Ein Würfel muss bei 100 Testwürfen höchstens 17 mal die 6 werfen, damit man einen gefälschten Würfel nur zu 3.76% passieren lässt.