Koordinaten der Eckpunkte C und D des Rechtecks ermitteln

Question

Aufgabe:

ermitteln Sie die fehlende Koordinaten der Punkte C und D.

Problem/Ansatz: Wie ich C ausrechnen muss weiß ich aber C mit 2 unbekannten nicht, wie kann ich es am besten herausfinden?

 

Answer 1

Merkwürdige Notation für Punkte.

Da alle Winkel in einem Rechteck 90° groß sind, muss der Winkel zwischen den Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{BC}\) dementsprechend auch 90° sein. Hierfür genügt es, wenn das Skalarprodukt beider Vektoren null ist:

\(\overrightarrow{AB} \circ \overrightarrow{BC} = 0 \Leftrightarrow \begin{pmatrix}-2\\ -4\\-4\end{pmatrix} \circ \begin{pmatrix}c_1+3\\ c_2+2\\-2\end{pmatrix} = 0 \\ \Leftrightarrow -2\cdot (c_1+3) -4\cdot (c_2+2) -4 \cdot (-2) = 0 \\ \Leftrightarrow -2(c_1+2c_2+3)=0\)

Außerdem soll die Länge des Vektors \(\overrightarrow{BC}\) halb so groß sein wie die von \(\overrightarrow{AB}\).

\(\sqrt{(-2)^2+(-4)^2+(-4)^2}= 2\cdot \sqrt{(c_1+3)^2+(c_2+2)^2+(-2)^2} \\ \Leftrightarrow 3=\sqrt{(c_1+3)^2+(c_2+2)^2+(-2)^2} \\ \Leftrightarrow (c_1+3)^2+(c_2+2)^2=5 \)

Die erste Gleichung stellt eine Gerade, die zweite einen Kreis dar, wobei die Gerade eine Sekante an dem Kreis ist.

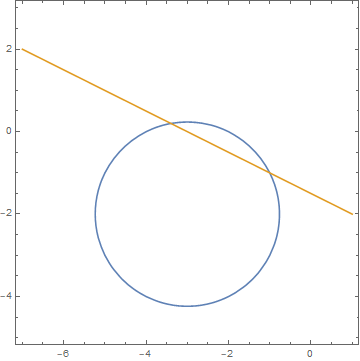
(c₁ auf der horizontalen, c₂ auf der vertikalen Achse)
Die resultierenden Lösungen (eine entfällt) lauten:
\(c_1=-\dfrac{17}{5} \,\wedge\, c_2=\dfrac{1}{5}\;\;\vee\;\; c_1=c_2=-1\)

Nun solltest du den vierten Eckpunkt bestimmen können.