Ermittele rechnerisch, welche Koordinaten die Eckpunkte dieses Rechtecks haben müssen, damit die Flächeninhalt …

Question

Aufgabe:

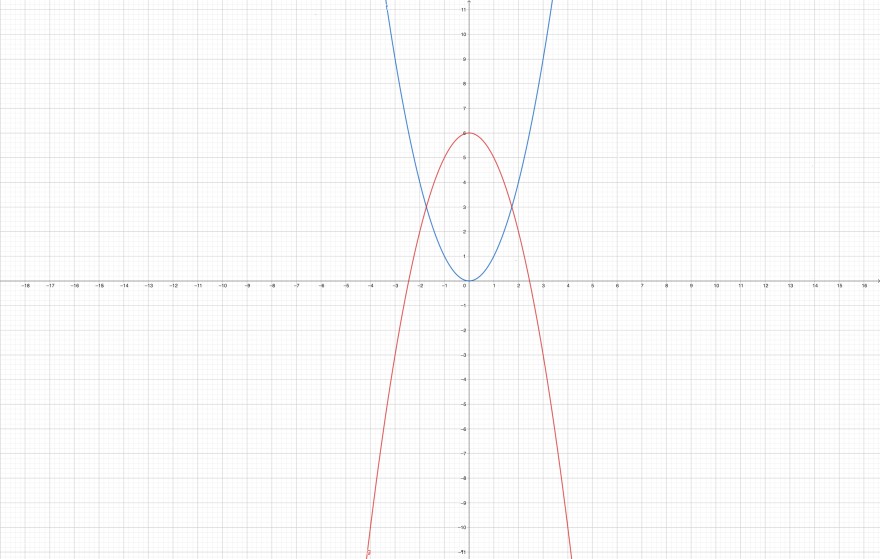
Die Parabeln zu den quadratischen Funktionen f mit f(x)=x^2 und g mit g(x)=6-x^2 schließen oberhalb der x-Achse ein Flächenstück ein. In dieses Flächenstück werden achsenparallele Rechtecke so gelegt, dass jeweils zwei Eckpunkte auf der gleichen Parabel liegen.

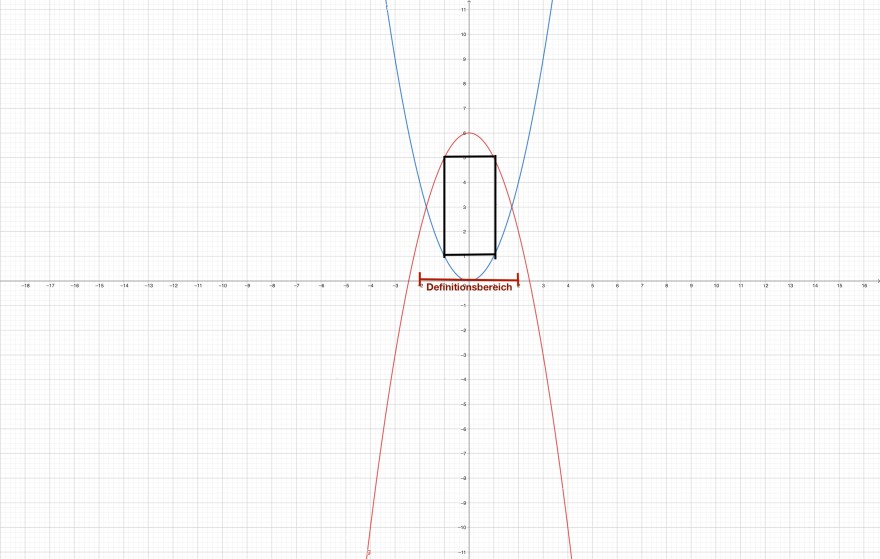
a) Fertige mit Hilfe der u.g Abbildung eine entsprechende Skizze an und bestimme einen sinnvollen Definitionsbereich

b) Ermittele rechnerisch, welche Koordinaten die Eckpunkte dieses Rechtecks haben müssen, damit die Flächeninhalt maximal wird?

Text erkannt:

W

Problem/Ansatz:

a)

Text erkannt:

I)

Definitionsbereich (-2 > a < 2)

b)

ich brauche Hilfe bei der Aufgabe b, da ich nicht weiß was ich machen muss.

Comments

Dein Definitionsbereich ist nicht sinnvoll. Er sollte von Schnittstelle zu Schnittstelle gehen. +2 und -2 sind nicht die Schnittstellen.

---

wie soll ich es denn aufnotieren? ich war mir nicht so sicher

---

Rechne aus, wo sich die Grafen schneiden (also wo x²=6-x² gilt).

Answer 1

Hallo,

den Flächeninhalt des Rechtecks kannst du berechnen mit

\(A=\overline{AB}\cdot \overline{BC}\)

mit \(\overline{AB}=2a\quad \overline{BC}=g(a)-f(a)\)

Also gilt für den Flächeninhalt \(A=2a\cdot (6-a^2-a^2)=-4a^3+12a\)

Bilde die 1. Ableitung, setze sie = 0 und löse nach a auf.

Gruß, Silvia

Answer 2

Schnittstellen:

x^2= 6-x^2

2x^2 = 6

x^2 = 3

x= +-√3

A(x) = x*(g(x)-f(x)) = x*(6-x^2-x^2) ) = 6x-2x^3

A'(x) = 0

6-6x^2=0

x^2= 1

x= +-1

Comments

Die Fragestellerin wird eine Weile grübeln müssen über den Unterschied von deiner und von Silvias Zielfunktion.

---

ich habe nicht ganz verstanden wie du auf die Zielfunktion gekommen bist

---

Kannst du bitte ein Bild schicken wie die Rechtecke platziert werden müssen

Answer 3

\(A(u)=2u*(6-u^2-u^2)=12u-4u^3\) soll maximal werden.

\(A´(u)=12u-12u^2\) 

\(12u-12u^2=0\)  \(u-u^2=0\)

\(u*(1-u)=0\)

\(u_1=0\)

\(u_2=1\)

\(P(1|1)\)  \(Q(1|5)\)  \(A(-1|1)\)  \(Q(-1|5)\)