Vom Duplikat:
Titel: Das Gauß-Verfahren für Determinanten
Stichworte: determinante,gaußsches-eliminationsverfahren,gauß
Aufgabe:
0 2 −3 −2
2 −3 1 2
−4 4 −2 −1
6 −4 3 2
Für diese Matrix soll die Determinante (Gauß-Verfahren) ausgerechnet werden.
Problem/Ansatz:
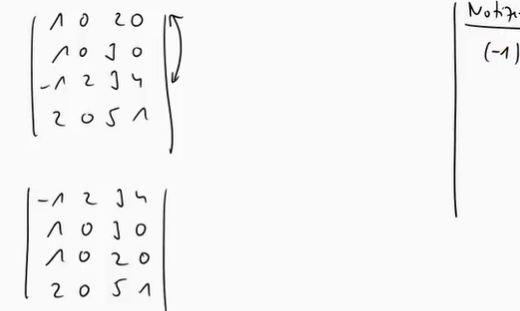
Hier sieht man, dass er nach einem Zeilen umtausch den Faktor (-1) mit nimmt, da sich die Determinante ändert.
Bei meiner Aufgabe, habe ich das Problem, wenn ich die 1.Zeile mit der 2.Zeile umtausche, ändert sich nicht die Determinante, sprich ich muss keine Zahl mitnehmen die am ende noch drauf multipliziert oder geteilt wird.