Vorab: Bitte versuche in Zukunft deine Funktionsgleichungen klarer darzustellen, denn es ist kaum ersichtlich, ob es sich bei z.B. f(x) um f(x)=0,5*2x handelt oder f(x)=0,5*2x=x. Notfalls LaTeX nutzen.
Ich gehe anhand deiner (richtig aufgestellten) Umkehrfunktionen mal davon aus, dass:
$$f(x)=0,5*2^x$$
$$g(x)=3*2^{-\frac{1}{2}x}$$
$$\overline{f}(x)=1+\log_{2}{x}$$
$$\overline{g}(x)=-2*\log_{2}{\frac{x}{3}}$$
Umkehrfunktionen verhalten sich so, dass sie die Definitionsmenge der ursprünglichen Funktion als Wertemenge, die Wertemenge der ursprünglichen Funktion als Definitionsmenge nutzen.
Das bedeutet folgendes:
$$D_{f}=\{x|x∈R\} ⇔ W_{\overline{f}}=\{y|y∈R\}$$
$$D_{g}=\{x|x∈R\} ⇔ W_{\overline{g}}=\{y|y∈R\}$$
$$W_{f}=\{y|y∈R, y>0\} ⇔ D_{\overline{f}}=\{x|x∈R, x>0\}$$
$$W_{g}=\{y|y∈R, y>0\} ⇔ D_{\overline{g}}=\{x|x∈R, x>0\}$$
Aus den Definitionsmengen der Umkehrfunktionen kannst du ablesen, dass du die Funktionen im 1. und 4. Quadranten zeichnen musst. Mache dir notfalls eine Wertetabelle und trage die Werte in das Koordinatensystem einfach ab :).
Mögliche (gute) x-Werte für f-1(x) sind 2n , da log2(2n)=n. Also z.B. x=2-2, x=2-1, x=1, x=2, x=4, x=8
Mögliche (gute) x-Werte für g-1(x) sind 3*2n , da $$ \log_{2}{\frac{3*2^n}{3}}=\log_{2}{2^n}=n$$
Also z.B. x=3*2=6, x=12, x=3*2-1 , x=3*2-2 , x=3
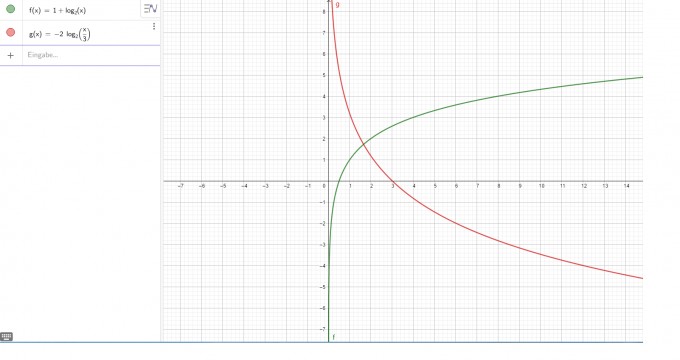
Du könntest natürlich alternativ auch die Funktionen f(x) und g(x) in das Koordinatensystem eintragen und an y=x spiegeln. Dabei müsstest du aber ebenfalls auf Definitions- und Wertemenge achten.
Sieht dann ungefähr so aus: