Schnittpunkt zweier Wendetangenten und Extremalproblem

Question

f(x)=sin(x)+sin(x-(^pi/₃)) gesucht ist der schnittpunkt beider wendetangenten..

 

Gegeben sind die graphen der beiden funktionen f(x)=sin(x) und g(x)=-sin(2x), 0 ≤ x ≤ pi. Wie muss x gewählt werden , wenn der betrag der ordinatendifferenz h der beiden kurven maximal werden soll?

 

Danke :))

Answer 1

f(x) = SIN(x)
g(x) = - SIN(2·x)

d(x) = f(x) - g(g) = SIN(x) + SIN(2·x)

d'(x) = COS(x) + 2·COS(2·x) = 0

COS(x) + 2·(2·COS(x)^2 - 1) = 0
COS(x) + 4·COS(x)^2 - 2 = 0

Substitution z = COS(x)

4·z^2 + z - 2 = 0
z = - √33/8 - 1/8 ∨ z = √33/8 - 1/8

x = arccos(- 1/8 + √33/8) = ± 0.9359294556
[x = arccos(- 1/8 - √33/8) = ± 2.573763280]

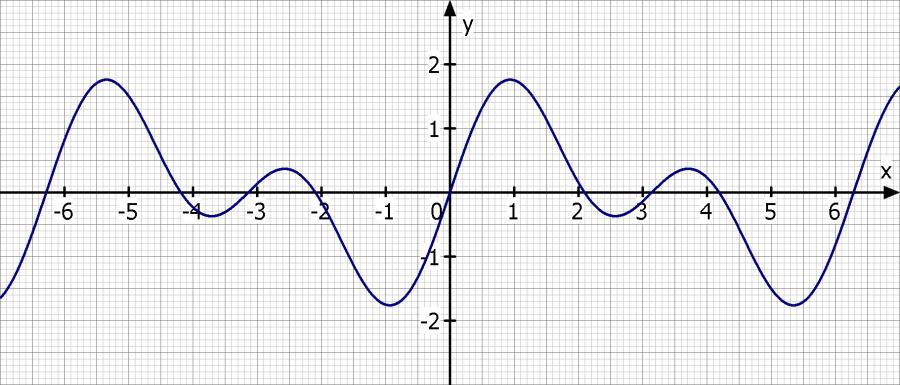
Skizze: