die parabel k ist das schaubild der funktion f mit f(x) = x² - 2x + 2,5
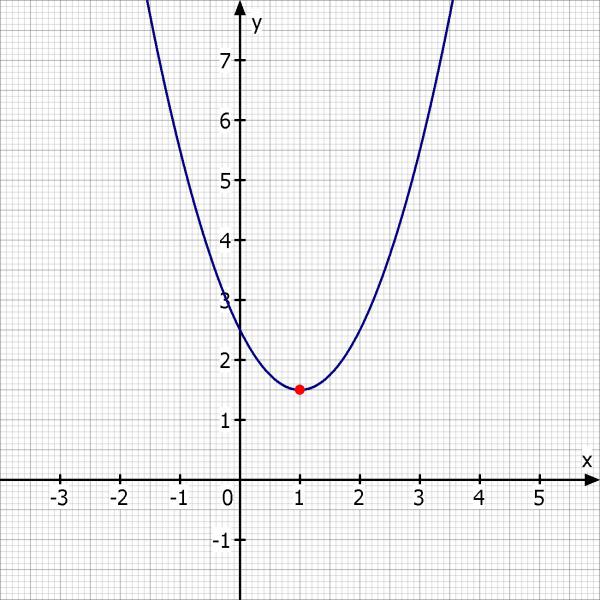
1) kennzeichnen sie den minimalen Funktionswert und bestimmen sie diesen
Sx = -b/(2a) = 1
Sy = f(1) = 1.5
wie entsteht K aus der normalparabel?
Wenn man die Normalparabel um 1 Einheit nach Rechts und um 1.5 Einheiten nach oben verschiebt.
2) für welche x-werte gilt f(x) > 2,5?
x < 0 oder x > 2
3) Verschieben Sie K so in y-richtung, dass die verschobene parabel g den punkt P(1/0) mit der x-achse gemeinsam hat. Wie liegt g im koordinatensystem?
Der Scheitelpunkt liegt dann auf der x-Achse.