Hallo :-)
Ich habe eine Aufgabe, welche ich bereits gelöst habe, aber dennoch unsicher bin, ob meine Lösung richtig ist.
Die Aufgabe:
Der Präsident weigert sich das Protokoll eines Telefonats mit einem anderen Staatsoberhaupt einem Untersuchungssausschuss des Abgeordnetenhauses auszuhändigen. Er erzählt folgende Ausrede: Gerade als er es abgeben wollte, kam ein wilder Stabschef vorbeigelaufen und hat das Protokoll in 12 Teile zerrissen. Zum Reparieren hatte der
Präsident leider nur einen Tacker mit 30 Heftklammern dabei. Er wollte jeweils zwei Teile zusammentackern, wenn sie eine gemeinsame Grenzlinie haben. Der Präsident behauptet die Heftklammern hätten nicht gereicht. Die Reste des Protokolls hat er weggeworfen.
Entlarve die Geschichte mit einem mathematischen Argument als Lüge.
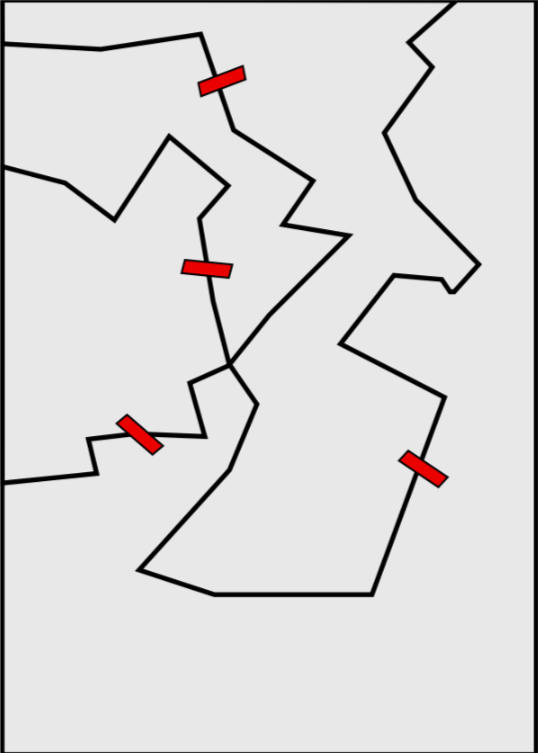
Das Bild zeigt ein Beispiel.
Aus der Vorlesung:
In der Vorlesung hatten wir bereits das Thema "Planare Graphen" und haben dabei die Eulersche Polyederformel besprochen. Aus dem Beweis von der Polyederformel haben wir daraus gefolgert, dass ein Planarer Graph mit n Knoten max. m ≤ 3*n-6 Kanten hat.
Meine Idee/Lösung:
Der Präsident hatte 12 Teile und 30 Heftklammern. Dabei behauptet er, dass am Ende die 30 Heftklammern nicht ausreichten die Teile wieder zusammen zu heften.
Ich würde sagen, dass wir somit einen planaren Graphen betrachten, mit 12 Knoten. und ein Planarer Graph hat nach der Folgerung der Polyederformel (Vorlesung) max. m ≤ 3*n-6 Kanten also wenn man die 12 Knoten als n hier einsetzt : m ≤ 30 Kanten.
Das bedeutet, dass die 30 Heftklammern vollkommen ausreichen würden, weil 12 Teile max. 30 Heftklammern benötigen.
Meine Frage:
Ist das richtig oder muss ich noch etwas beweisen ? Und muss ich die "richtige" Polyederformel auch anwenden?
( "Richtige" Polyederformel: Sei der Graph ein zusammenhängender ebener Graph. Dann gilt:
Anzahl der Gebiete = Kardinalität von Kanten - Kardinalität von Knoten + 2)
Danke für eure Hilfe im voraus! :-)