Funtionsterm von Polynom anhand von Graphen bestimmen?

Question

Aufgabe:

Funtionsterm anhand von Graphen bestimmen:

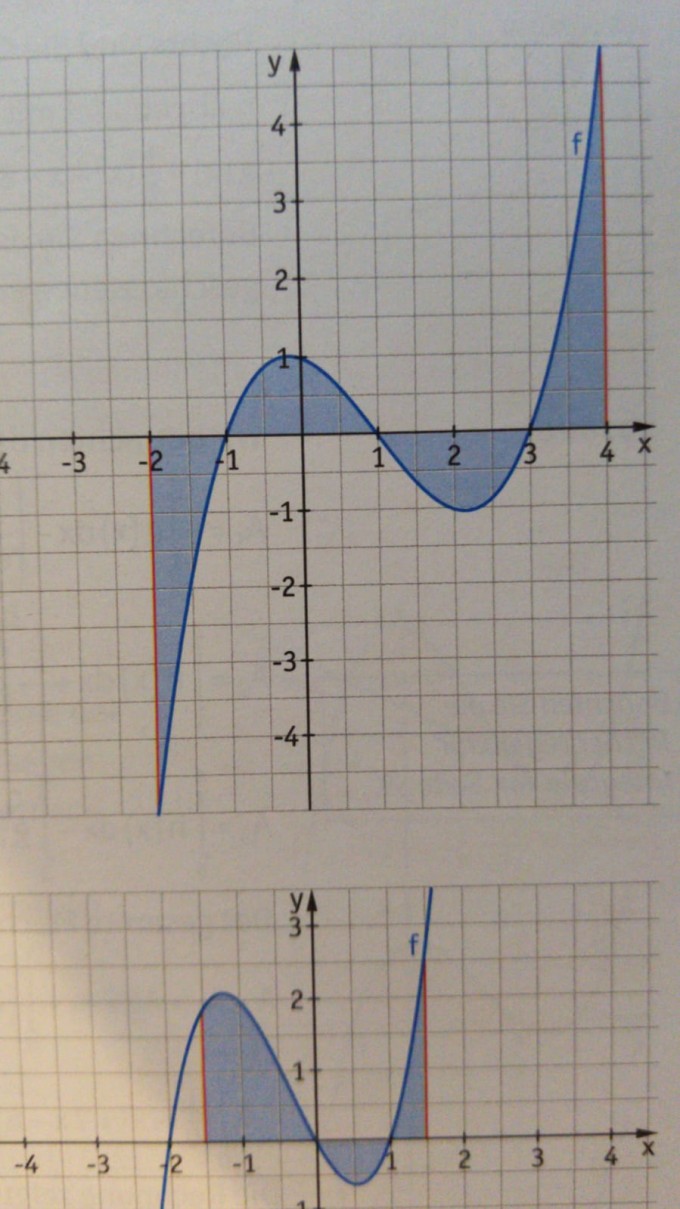
Problem/Ansatz:

Ich hätte zwei Ansätze (einmal Linearfaktorzerlegung oder mit der Matrix).

Jdoch habe ich ein Problem bei beiden Wegen: Wenn ich Punkte bestimmen möchte für die Matrix, dann hab ich kein HP und kein TP (weil keine genaue Bestimmung und wenn ich es mit den Nullstelen eine Matrix und den Wendepunkt rechne, komme ich auch auf keine Funktion (GTR-Weg)

Bei der Linearfaktorzerlegung, hätte ich aber nicht die Verschiebung (weil man auch wenn man F(X)=0 setzt, eine falsche funktion herausbekommt:

Der Punkt P(0/1) wird nicht berührt oder? Welche Punkte dürft ich mit der Matrix überhaupt nehmen? Und wie kann ich das richtige Ergebnis mit der Linearfaktorzerlegung bestimmen ( Danach sollten wir übrigens die Fläche bestimmen)

Answer 1

Hallo

 1. wenn man nur den Graphen, und den nur stückweise kennt kann man eine Funktionsgleichung nur unter zusätzlichen Annahmen bestimmen.

 anscheinend geht die funktion für pos große x nach +oo für negative nach -oo , und sie hat 2 Extremwerte. dann ist die einfachsten mögliche funktion ein Polynom dritten Grades (könnte aber auch 5 ten oder 7 ten Grades sein. sie schein symmetrisch zu x=1 falls als 3 ten Grades ist da ein Wendepunkt, ausserdem hat man 3 Nullstellen anscheinend auch noch die Fläche zwischen den Linien?

damit hat man als einfachste Fkt. f(x)=a*(x+1)*(x-3)*(x-1) und muss nur noch a aus dem Wendepunkt bei x=1 oder einen Punkt ablesen etwa bei x=4 oder -2

wenn du mit Matrix meinst Punkte in die allgemeine Gleichung einsetzen ist das ja umständlicher, aber sonst natürlich richtig.

Gruß lul

Answer 2

f(x) = a·(x + 1)·(x - 1)·(x - 3)

f(0) = a·(0 + 1)·(0 - 1)·(0 - 3) = 1 --> a = 1/3

f(x) = 1/3·(x + 1)·(x - 1)·(x - 3) = 1/3·(x^3 - 3·x^2 - x + 3)

g(x) = a·(x + 2)·x·(x - 1)

g(-1) = a·(-1 + 2)·(-1)·(-1 - 1) = 2 → a = 1

g(x) = (x + 2)·x·(x - 1) = x^3 + x^2 - 2·x

Comments

Aber Warum 1 geht der denn genau durch den Punkt 1?

---

Da keine Punkte angegeben sind, darfst du annahmen machen.

Natürlich weiß man nicht das es genau der Punkt (0 | 1) ist. Es könnte auch (0 | 1.00000025) sein. Aber es ist wohl annehmbar das der y-Achsenabschnitt genau bei 1 ist oder?

---

Hallo

 mit a=1/3 liegt der Wendepunkt auch bei x=1 und die Werte y=5 bei x=4 und -2 stimmen auch mit der Zeichnung überein. sowas kann man ja noch überprüfen, wenn man f(0)=1 abgelesen hat.

Gruß lul

Answer 3

Geh zur Ermittlung des Funktionsterms wie im ersten Beispiel
vor
3 gut ablesbare Nullstellen
( x | y )
( -2 | 0 ) => ( x + 2 ) = 0
( 0 | 0 )  => ( x + 0 ) = 0 
( 1 | 0 )  => ( x - 1 ) = 0
f ( x ) = a * ( x + 2 ) * x * ( x -1 )
Mit am besten ablesbar
( 1.5 | 2.5 )
f ( 1.5 ) = a * ( 1.5 + 2 ) * 1.5 * ( 1.5 -1 ) = 2.5
a * 3.5 * 1.5  * 0.5 = 2.5
a * 2.625 = 2.5
a = 0.952

f ( x ) = 0.952 * ( x + 2 ) * x * ( x -1 )