Aufgabe:
Gegeben sind die Stützstellen t1=0, t2=1/2 und t3=1. Skizzieren Sie das Lagrange-Polynom
$$ L_{1}(t)=\frac{\left(t-t_{2}\right)}{\left(t_{1}-t_{2}\right)} \frac{\left(t-t_{3}\right)}{\left(t_{1}-t_{3}\right)} $$
und die genaue Lage der Bézier-Punkte b0, b1 und b2 dieser Kurve L1(t). Hinweis: b1 lässt sich aus der Ableitung am Rand ermitteln.
Problem/Ansatz:
Die Lösung habe ich bereits da. Die Frage ist wie kommt man auf die Formel L1(t) = 2t2 -3t+1 und auf L'1(0)=-3
Wie findet man genau die Punkte b0, b1, b2 raus? Was ist mit Tangente führt direkt zu b1 gemeint?
Als Antwort habe ich im Script:
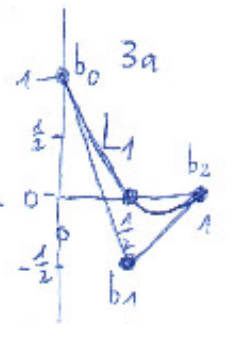
L1(t) = 2t2 -3t+1, L'1(0)=-3 (Tangente führt direkt zu b1=[1/2, -1/2]T, vgl. Skizze)
Skizze: