Fußball - Satz des Pythagoras

Question

Das Tor ist 2,44 m hoch und 7, 32 m breit. Vor dem Tor befindet sich mit 5, 50 Abstand nach vorne und jeweils vom Torpfosten aus an der Grundlinie 5,50 m nach rechts bzw. nach links der rechteckige, sogenannte "5 m - Raum", in dem der Torwart besonderen Schutz genießt. a) Wie weit ist es für den Torwart von der Mitte seines Tores bis zu den Eckpunkten des 5 m - Raumes? b) Wie weit muss der Torwart vom rechten Torpfosten aus zu den Eckpunkten des 5 m - Raumes laufen? c) Ein Stürmer schießt den Ball vom Eckpunkt des 5 m - Raums geradlinig ins "lange obere Eck". Wie weit fliegt der Ball, bis er die Torlinie überquert hat?  )

Answer 1

Hier eine kleine Skizze:

 

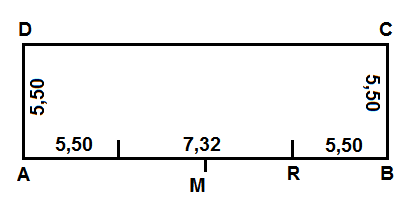
zu a)

MB = MA = 5,5 + 7,32 / 2 = 9,16

MC = MD = √ ( MB ² + BC ² ) = √ ( 9,16 ² + 5,50 ² ) = 10,64 m (gerundet)

 

zu b)

RA = 5,50 + 7,32 = 12,82 m

RB = 5,50 m

RC = √ ( RB ² + BC ² ) = √ ( 5,50 ² + 5,50 ² ) = 7,78 m (gerundet)

RD = √ ( RA ² + AD ² ) = √ ( 12,82 ² + 5,50 ² ) = 13,95 m (gerundet)

 

zu c)

Bezeichnet man das rechte obere Toreck (dort wo der Punkt R eingezeichnet ist) mit T, und nimmt man an, dass der Stürmer vom Punkt D aus schießt, dann ist die geradlinige Entfernung, die Der Ball bis zur Überquerung der Torlinie zurücklegen muss:

DT = √ ( DA ² + RA ² + Torhöhe ² ) = √ ( 5,50 ² + 12,82 ² + 2,44 ² ) = 14,16 m (gerundet)

Auf diese Weise kann der Satz des Pythagoras ins Dreidimensionale und auch in noch höhere Dimensionen fortgesetzt werden.