Text erkannt:
\( \mathbb{R}^{\wedge} \sim \uparrow \)
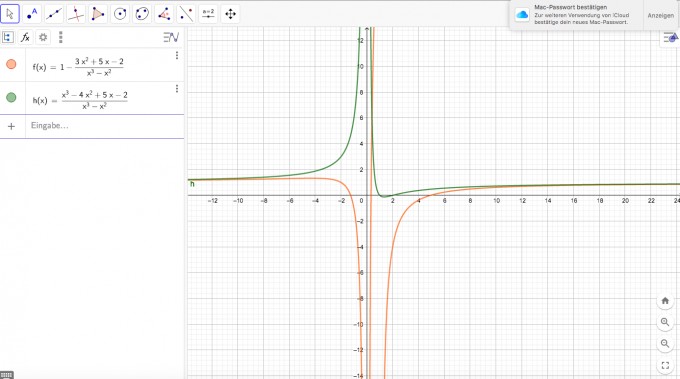
\( f(x)=1-\frac{3 x^{2}+5 x-1}{x^{3}-x^{2}} \)
\( h(x)=\frac{x^{3}-4 x^{2}+5 x}{x^{3}-x^{2}} \)
meine Frage wäre:
Es geht um gebrochen-rationale Funktionen.
Wenn ich ja den Zähler der Ausgangsfunktion durch den Nenner teile (Polynomdivision), erhalte ich ja die Asymptote + den Restterm.
Ich frage mich jedoch, warum sich der Verlauf der beiden Graphen unterscheidet (siehe Grafik oben) , also die Ausgangsfunktion im Vergleich zur Funktion nach der Polynomdivision.
Die beiden Graphen müssten doch eigentlich gleich verlaufen, sie wurden ja nur umgeschrieben, oder liege ich da falsch?