Aufgabe (Graphen von sin und cos):
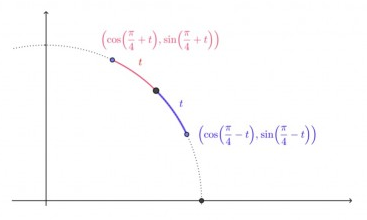
Übertragen Sie die folgende Zeichnung am Einheitskreis auf Ihr Arbeitsblatt und erläutern Sie anhand einer kurzen geometrischen Überlegung: Für \( 0 \leq t \leq \frac{\pi}{4} \) gilt
$$ \sin \left(\frac{\pi}{4}+t\right)=\cos \left(\frac{\pi}{4}-t\right) \quad \text { und } \quad \cos \left(\frac{\pi}{4}+t\right)=\sin \left(\frac{\pi}{4}-t\right) $$
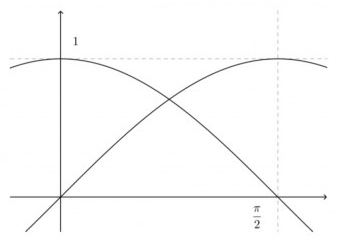
Unten sehen Sie Ausschnitte der Graphen von sin und cos. Welcher Graph gehört zu welcher Funktion, und welche Eigenschaft der Graphen spiegelt die oben angegebenen Identitäten wider?