Wieviele Murmeln passen in einen Würfel?

Question

Aufgabe:

Ein Würfel mit 10cm Kantenlänge wird mit Murmeln gefüllt. Die Murmeln haben einen Durchmesser von 1cm. Wieviele Murmeln passen rein?

Es sollten ja mehr als 1000 reinpassen, da ja die Dellen besetzt werden können.. Kubisch dichteste Packung...

Gibt es das eine exakte Lösung? Wie wird das denn gerechnet?

Answer 1

Schau mal hier:

https://de.wikipedia.org/wiki/Dichteste_Kugelpackung

Comments

Das hatte ich auch gesehen, aber gilt ja nur für unendliche Packungen und nicht für Grenzen, hier 10cm Kantenlänge, oder sehe ich das falsch?

Was ist denn hier optimaler? Wurstpackung (linear) oder Kubisch dichteste Packung oder hexagonal dichteste Packung?

---

Du hast recht. Der Link hilft nicht weiter. Es ist so: In den Würfel passen 6 Schichten zu 10·10 Kugeln und 9 Schichten zu 9·9 Kugeln, also 1005 Kugeln.

---

Du meinst also eine Packungsabfolge ABC 5 mal und nochmal A ...

kann man irgendwie rechnen, das die Gesamtdicke < = 10 cm ist?

---

1005 Kugeln

Das ist doch viel zu wenig

---

Ich meine dies:

---

das was du gezeichnet hast ist aber AB Schichtung = hexagonale Packung.

Die Frage ist ja, wieviele Schichten bekommt man auf 10 cm?

Linear ist einfach, also 10 Schichten a 10x10 Kugeln.

Wenn man auf 11 Schichten käme, wären das 6 mal 100 und 5 mal 81 also 1005 insgesamt.. so wie du gesagt hast.

Die Frage ist nur ob diese 11 Schichten weniger oder gleich 10 cm hoch sind... ‍♂️

---

Na, das ist doch trivial.

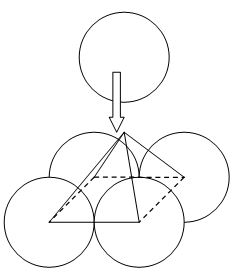
4 Kugeln einer Schicht sind so angeordnet, dass ihre Mittelpunkte ein Quadrat mit der Seitenlänge 2r = 1cm bilden.

Die 5. Kugel ist so von oben abzusenken, dass sie jede der 4 Kugeln berührt.

Verbindet man den Mittelpunkt dieser 5. Kugel mit den Mittelpunkten der 4 Kugeln, entsteht eine gerade quadratische Pyramide, deren schräge Kanten ebenfalls die Seitenlänge 2r=1cm haben. Diese Pyramide hat nach Pythagoras die Höhe 0,5√2.

Das ist der Abstand der beiden Ebenen, die denen die Mittelpunkte der Kugeln einer Schicht und die Mittelpunkte der Kugeln der benachbarten Schicht liegen.

---

Wenn man berechnet hat, ob ein Wechsel aus 10 mal 10-Schichten und 9 mal 9 Schichten Platz für 11 Schichten hat, sollte man prüfen, ob in 11 Schichten auch ein Wechsel aus 10 mal 10-Schichten und 9 mal 10 Schichten höhenmäßig passt.

---

Perfekt, danke, das ist die Antwort die ich gesucht habe.

Jetzt kann mein Sohn die Mathelehrerin, die er nicht mag kitzeln...

---

Ich glaube, es passen sogar 13 Schichten aufeinander:

7 Schichten 10·10=700

6 Schichten 9·9=    486

Also zusammen      1186

---

Also ich komme auf 12 Schichten:

Die Höhe einer Pyramide vom Mittelpunkt zum Mittelpunkt der oberen Schicht ist ja 0,5 Wurzel(2). Also ca. 0,71. Für die Oberste und Unterste Schicht kommen nochmal 0.5 vom Mittelpunkt bis zum Boden bzw. Deckel.

Also n=(10-2r)/Wurzel(2)/2

Kommt ca. 12,7 raus. Entsprechend 12 ganze Schichten.

6 x 10x10 + 6 x 9x9 = 1086 Murmeln

---

Mittelpunkte der 1. Schicht auf Höhe 0,5

Mittelpunkte der 2. Schicht auf Höhe 0,5+√2/2

Mittelpunkte der 3. Schicht auf Höhe 0,5+2·√2/2

.

.

.Mittelpunkte der n. Schicht auf Höhe 0,5+ (n-1)·√2/2

Dann noch 0,5 von n-ter Schicht bis Deckfläche.

Ansatz: 1+ (n-1)·√2/2=10

Lösung: 13<n <14