Konvergenz von einer Reihe mit limes

Question

Wieso konvergiert diese Reihe gegen 0?

\( \sum \limits_{k=1}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) ! n^{2 k}} \)

mit lim n -> unendlich

Comments

Wo genau kommt das x im Zähler her?
Gehen wir davon aus, das ist eine Konstante:
Der Zähler ist fix, der Nenner geht jedoch gegen unendlich, weil n^2k mit n->∞ maximal wird. Somit wird der gesamte Bruch 0. Und da ist die Reihe nebensächlich.

---

Meine Aufgabe lautet:

Zeigen Sie:

lim n->∞ n*sin(x/n)=x

Für alle x Element reeler positver Zahlen

Da:

 

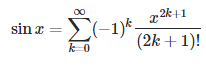
Text erkannt:

\( \sin x=\sum \limits_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) !} \)

 kommt mit Umformungen:

Text erkannt:

\( \sin x=\sum \limits_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) !} \)

 

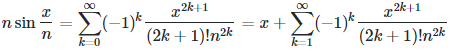
Text erkannt:

\( n \sin \frac{x}{n}=\sum \limits_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) ! n^{2 k}}=x+\sum \limits_{k=1}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) ! n^{2 k}} \)

 raus. also muss diese summe gegen 0 konvergieren  (tut es auch habe es im Internet es kontrolliert).

Aber wieso es gegen 0 konvergiert kein Plan.

Text erkannt:

\( \sin x=\sum \limits_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) !} \)

Answer 1

Meine Aufgabe lautet:

Zeigen Sie:

lim n->∞ n*sin(x/n)=x

Und für diese Banalität veranstaltest du so einen Reihen-Overkill?

Wir haben bereits in der 12. Klasse gelernt und nachgewiesen (allerdings vor 40 Jahren), dass \( \lim\limits_{x\to0}\frac{sin(x)}{x}=1 \) gilt.

Comments

Ok das macht das ganze natürlich einfacher, vielen Dank für die Antworten.