Zwei Stäbe der Längen a = 27 cm und b = 21 cm sollen ohne Verwendung einer Messvorrichtung nur mit Hilfe einer Säge in möglichst viele gleichlange Teile zersägt werden. Die praktische Durchführung gelingt, wenn man die Stäbe an einer Seite bündig aneinanderlegt und den Überstand ü = a – b vom längeren Stab abtrennt. Unter den so erhaltenen Stücken wählt man die beiden kürzesten und verfährt mit ihnen so, wie mit den ersten beiden gegebenen Stücken. Auf diese Weise ist ein rekursives Verfahren beschrieben, das in unserem Beispiel endet, wenn zunächst ein Stück und später alle Stücke die Länge 3 haben.
Die Stablängen, die sich dabei als Überhänge ergeben, sind:
6, 15, 9, 3, 3, …
Man erkennt, dass 3 der größte gemeinsame Teiler von 27 und 21 und dass das rekursive Verfahren der Euklidische Algorithmus ist.
Für rationale Zahlen p und q führt der Euklidische Algorithmus zum sogenannten „gemeinsamen Maß“ von p und q.
Zum Beispiel seien p = 3/2 und q = 7/3. Dann führt der Euklidische Algorithmus nacheinander zu 5/6, 2/3, 1/6, ½, 1/3, 1/6, 1,6, …
Rechnerisch endet das Verfahren, wenn im Vergleich der beiden kürzesten Stäbe ein Überstand von ü = 0 entsteht. Das gemeinsame Maß ist die kleinste positive Zahl, die im Laufe des Rekursionsverfahrens erreicht wird.
Mathematisch interessant wird die Rekursion dann, wenn statt rationaler oder natürlicher Längen mindestens eine der Längen irrational ist. Wählen wir zum Beispiel die Längen von Diagonale und Seite des Einheitsquadrates.
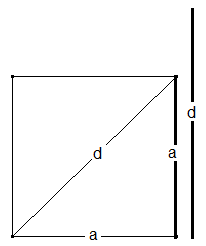
Für a = 1 und d = √2 sind die Stablängen nacheinander:
√2 – 1,
1 – (√2 – 1) = 2 – √2
(2 - √2) – (√2 – 1) = 3 - 2√2
(√2 – 1) – (3 - 2√2) = 3√2 – 4
(3√2 – 4) - (3 - 2√2) = 5√2 – 7
und so weiter und so weiter.
Jedes zweite Glied dieser Folge greifen wir heraus und erhalten:
√2 – 1,
3 - 2√2 = (√2 – 1)2
5√2 – 7 = (√2 – 1)3
und so weiter und so weiter.
Die Folge aus den ungeraden Gliedern der Stablängen beim Euklidischen Algorithmus bildet eine geometrische Folge. Dies ist leichter einzusehen, wenn man von einem DIN-Papierformat mit den Seitenlängen a und a√2 zunächst ein Quadrat der Seitenlänge a abschneidet und ein Rechteck ABCD erhält. Darin sei a als Längeneinheit definiert:
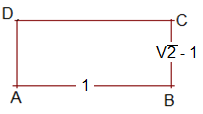
Von diesem Rechteck kann man zwei Quadrate der Seitenlänge √2 – 1 abschneiden, um das Rechteck EFGH zu erhalten:
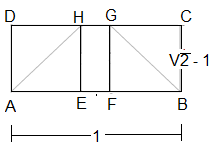
Nun lässt sich zeigen, dass die Rechtecke ABCD und EFGH ähnlich zueinander sind und eine Folge von Rechtecken durch wiederholtes Abschneiden jeweils zweier Quadrate konstruierbar ist. Die Seitenlängen dieser Folge von Rechtecken, sind in folgender Tabelle dargestellt:
Rechteck
| längere Seite
| kürzere Seite
|
ABCD
| 1
| √2-1
|
EFGH
| √2-1
| 3-2√2
|
JKLM
| 3-2√2
| 5√2-7
|
Allgemein an= (√2-1)n-1 (√2-1)n
In der oben konstruierten Folge von Stablängen nach dem Euklidischen Algorithmus liegt also eine geometrische Folge von Stablängen. Wegen q = √2 – 1 < 1 ist dies eine Nullfolge, die jedoch Null nie erreicht. Das verwendete Verfahren zur Bestimmung eines gemeinsamen Maßes bricht nie ab. Damit drängt sich ein begründeter Verdacht auf, dass 1 und √2 kein gemeinsames Maß haben. Man darf deshalb 1 und √2 als inkommensurabel (nicht messbar/vergleichbar) bezeichnen.
Man kann das hier gewonnene Verfahren auch nutzen, um näherungsweise Bruchdarstellungen mit guter Abschätzung des Fehlers zu erzeugen. Der Taschenrechner liefert:
(√2 – 1)20 ≈0,0000000221
Durch wiederholtes Anwenden einer binomischen Formel erhalten wir exakt
(√2 – 1)20=(√2 – 1)16·(√2 – 1)4=22619537 – 15994428∙√2
und daraus dann die ungefähre Gleichung
22619537 - 15994428∙√2 ≈ 0,0000000221
Die Auflösung nach √2 ergibt dann die Differenz aus einem Bruch (Näherungswert für √2 in Bruchdarstellung) und einer Zahl unter 10 –14 (Fehlerabschätzung).
Die Annahme, dass der Fehler gleich Null werden könnte, führt zu a – b√2 = 0 und dann zu √2 = a/b, wobei nach vollständigem Kürzen entweder a oder b ungerade ist. Quadrieren ergibt dann 2 = a2/b2, was aber ein Widerspruch zur Annahme des vollständigen Kürzens von a/b ist.