Ordne 5 Punkte auf einem Kreis so an, dass jeder von seinen Nachbarn den gleichen Abstand hat und benenne die Punkte gegen den Uhrzeigersinn fortlaufend und mit 0 beginnend mit den natürlichen Zahlen. Dann erscheint der Zahlenstrahl aufgewickelt auf einen Kreis.
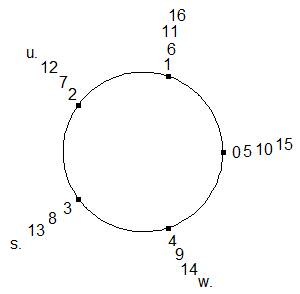
Stelle jetzt die Folge der geraden Zahlen auf diesem aufgewickelten Zahlenstrahl so dar, dass zwei aufeinanderfolgende Glieder durch eine Strecke verbunden sind.
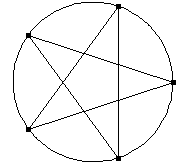
Es entsteht ein Pentagramm, das immer wieder durchlaufen wird, wenn wir die Folge der geraden Zahlen fortgesetzt darstellen.
Stellen wir jetzt die Folge der durch 3 teilbaren Zahlen in der gleichen Weise dar, entsteht nichts Neues. Das Pentagramm wird allerdings in der Gegenrichtung durchlaufen.
Nun erhöhen wir die die Anzahl der Punkte auf dem Kreis auf 7 und stellen wiederum die Folge der geraden bzw. die Folge der durch 3 teilbaren Zahlen dar. Dann entstehen zwei verschiedene siebenzackige Sterne:
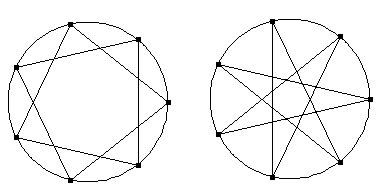
Sei k die Anzahl der Punkte auf dem Kreis und d die konstante Differenz einer arithmetischen Reihe. Dann drängen sich Fragen auf:
1. Welche Eigenschaften muss das Paar (k|d) haben, damit alle k Punkte auf dem Kreis erreicht werden?
2. Für welche Wahl von d ergeben sich bei festem k die gleichen Darstellungen der Folgen?
Interessanter wird eine derartige Darstellung geometrischer Folgen.
Seien 11 Punkte auf dem Kreis verteilt und die Folge der Potenzen von 2 (20, 21, 22, 23, 24, …) wird dargestellt:
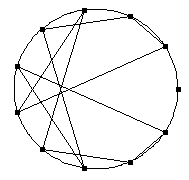
Seien 101 Punkte auf dem Kreis verteilt und die Folge der Potenzen von 2 (20, 21, 22, 23, 24, …) wird dargestellt:
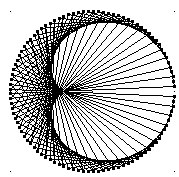
Hier ergeben sich deutlich schwierigere Fragen:
- Für welche Zahlen k (Anzahl Punkte auf dem Kreis) hüllt die Folge der Zweierpotenzen (2n)nєN in der beschriebenen Darstellung die Kardioide ein?
- Für welche Basis n hüllt die Darstellung der Folge der Potenzen von n eine Nephroide oder ein Kleeblatt ein?
Während die Beantwortung der Fragen zur arithmetischen Folge noch mit elementarer Zahlentheorie gelingt, müssen zur Beantwortung der zuletzt gestellten Fragen vertiefte Kenntnisse der Zahlentheorie eingesetzt werden. Insbesondere gibt es einen Zusammenhang zum Begriff ‚Primitivwurzel‘.