Berechnen von Flächeninhalten: f(x) = -x^2 + 5x -6 [0;4]

Question

Geben Sie eine Stammfunktion zu f an und berechnen Sie den Flaecheninhalt der Flaeche , die der Graph der Funktion f ueber em angegeben Intervall mit der x-Achse einschlaegt.

f(x) = -x^2 + 5x -6  [0;4]

Comments

die der Graph der Funktion f ueber em angegeben Intervall mit der x-Achse einschlaegt.

Steht da?

die der Graph der Funktion f über dem angegeben Intervall mit der x-Achse einschliesst.

---

@Lu oh mein gott ja stimmt sorry bin irgendwie in der aufgabe verrutscht :/ :)

---

fein, dann man wohl die nullstellen x₁, x₂ berechnen(auch wenn man sie ablesen kann) und dann von x₁ bis x₂ integrieren.

---

ok danke euch beiden habs jetzt hingekriegt :)

---

supie! ^^

:-)

Answer 1

hi

∫-x^2 +5x -6 dx = -x^3/3 + 5x^2/2 - 6x + C

(von 0 bis 2)∫-x^2 +5x -6 dx = [-x^3/3 + 5x^2/2 - 6x] ( von 0 bis 2 ) =

-2^3/3 + 5*2^2/2 - 6*2- (0^3/3 + 5*0^2/2 - 6*0) =

-8/3 + 20/2 - 12 - (0) =

-14/3

Comments

warum von 0-2 ? :) weil das intervall ist ja von 0-4

---

:D

oh, sorry, das war ja eine andere aufgabe. okay, setzen wir 4 ein:

(von 0 bis 4)∫-x² +5x -6 dx = [-x³/3 + 5x²/2 - 6x] ( von 0 bis 4 ) =

-4³/3 + 5*4²/2 - 6*4- (0³/3 + 5*0²/2 - 6*0) =

-64/3 + 80/2 - 24 - (0) =

-64/3 + 80/2 - 24 - (0) =

-128/6 + 240/6 - 144/6 - (0) =

-32/6 =

-16/3

 

---

ah ok super danke war schon irritiert :D

---

@dumminmathe

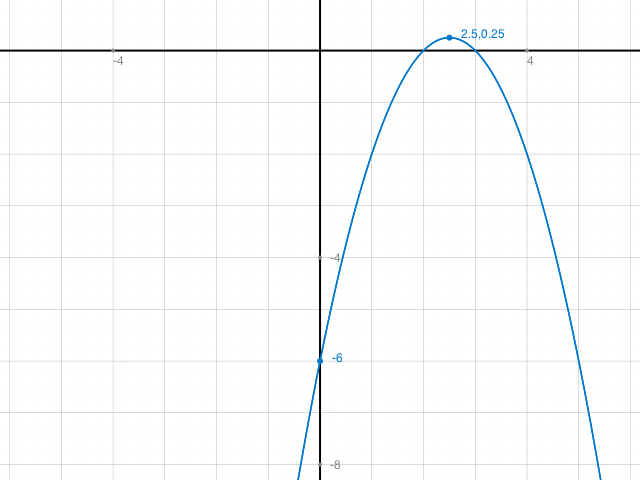
Mach dir in solchen Fällen immer erst eine Skizze

Du solltest die Grenzen 2 und 3 nehmen, wenn da eine Fläche über der x-Achse gesucht ist

Das kannst du aber mit Hilfe der Stammfunktion von Gorgar bestimmt selbst berechnen.

oder: Falls da etwas anderes in der Frage steht. Zusätzlich noch von 3 bis 4 integrieren.

Und dann die Beträge (d.h. minus weglassen) aller 3 Resultate addieren.

---

verdammt, da habe ich gerade gar nicht dran gedacht! ja, eine skizze ist schon sehr nützlich.