Angenommen, der rote Graph ist gegeben:
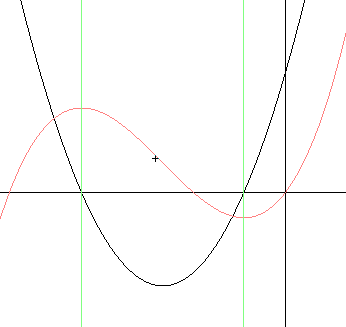
Dann hat seine Ableitung (schwarz) an den Extremstellen des roten Graphen Nullstellen. An der mit + bezeichneten Stelle fällt der rote Graph an stärksten. Dort hat seine Ableitung ein Minimum. Wähle weitere Punke des roten Graphen und schätze die Steigung an diesen Stellen. Trage die Werte der Steigungen an diesen Stellen ein. Verbinde die Punkte elegant.