Hallo,
... nur 3 ist rechts und y links
da es sich um ein Rechteck handelt, ist das das gleiche. Im Übrigen spielen die angegebenen Maße gar keine Rolle. Betrachte die Winkel der Dreiecke
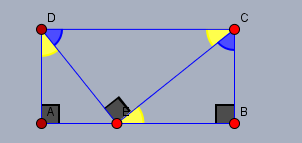
a) Zwei Dreiecke sind ähnlich, wenn sie in zwei Winkeln überein stimmen. Alle Dreiecke sind rechtwicklige, somit müssen wir nur noch einen gemeinsamen Winkel finden. \(\angle BEC = \angle DCE\) (gelb) sind Wechselwinkel an Parallelen und somit gleich. Folglich sind die Dreiecke \(\triangle EBC\) und \(\triangle DEC\) ähnlich.
Daraus folgt dann auch gleich, dass die blauen Winkel gleich groß sein müssen. Und da die Summe der beiden nicht-rechten Winkel in einem rechtwinkligen Dreieck immer 90° ist, ist auch \(\angle ADE = \angle DCE\) (gelb). Folglich sind alle drei Dreiecke ähnlich.
b) \(y\) ist \(=3\), da gegenüberliegende Seiten im Rechteck gleich lang sind. Und wenn man den Pythagoras für die Dreiecke \(\triangle ECD\) und \(\triangle AED\) aufstellt, erhält man $$\begin{aligned} w^2 = |DE|^2 &= x^2 - 5^2 \\ w^2 = |DE|^2 &= 3^3 + z^2 = 3^2 + (x-4)^2 \\ \implies x^2 - 5^2 &= 3^2 + (x-4)^2 \\ x^2 - 5^2 &= 3^2 + x^2 - 8x + 4^2 \\ 8x &= 3^3+4^2 +5^2 = 50 \\ x &= \frac {25}4\end{aligned}$$Dann ist $$z = \frac {25}4 - 4 = \frac 94 \\ w = \sqrt {3^2 + \left( \frac 94\right)^2} = \frac {15}4$$
Gruß Werner