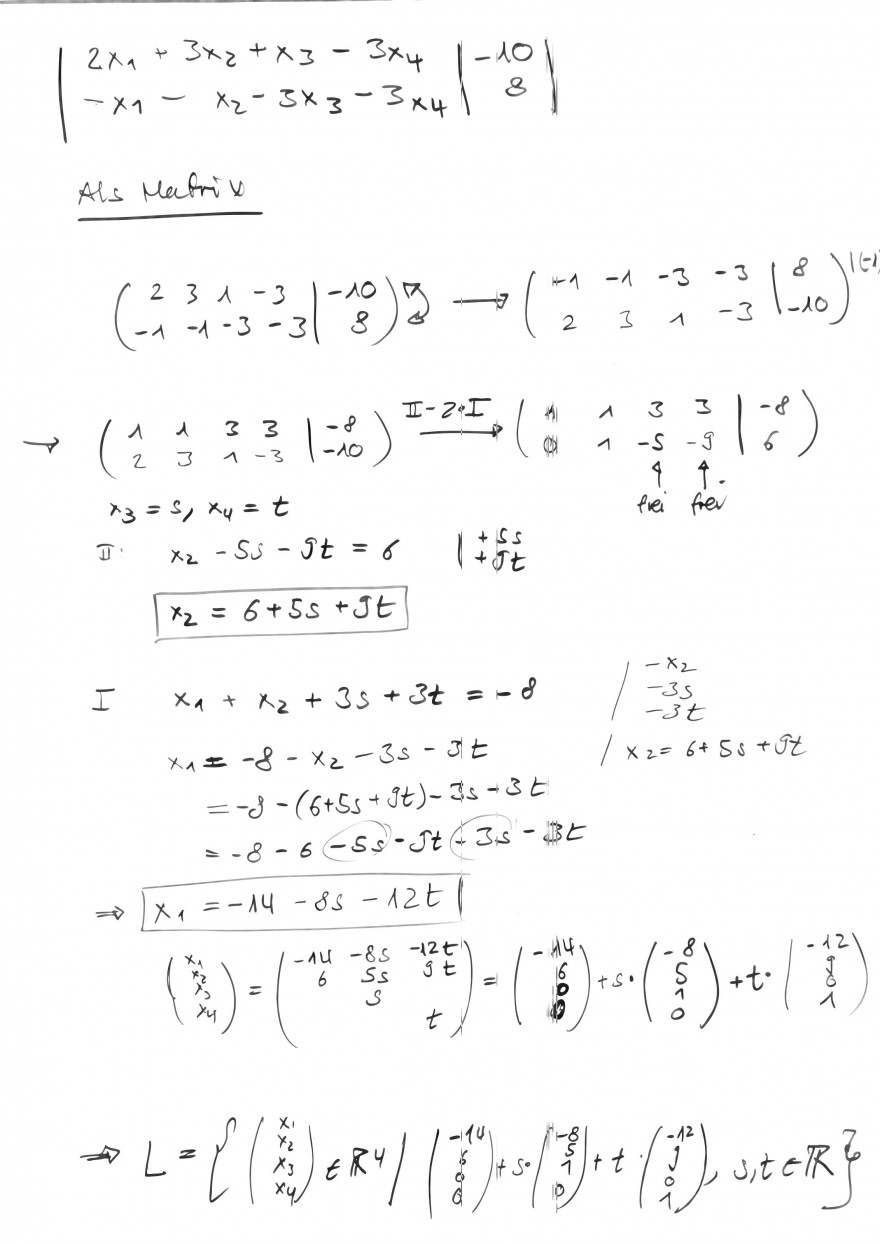Parameterdarstellung für die Lösungsmenge des folgenden Gleichungsystems.

Question

Aufgabe:

Man gebe eine Parameterdarstellung fur die Lösungsmenge des
folgenden inhomogenen Gleichungssystems in \(\mathbb{R}^4\) an:

\(2 x_{1}+3 x_{2}+x_{3}-3 x_{4}=-10\)
\(-x_{1}-x_{2}-3 x_{3}-3 x_{4}=8\)

Problem/Ansatz:

Ich bin mir nicht sicher, was gesucht ist aber ich habe das Gleichungssystem ganz normal per Gauss gelöst und \(x_3 = s\) und \(x_4 = t\) gesetzt. Also Parametrisiert. 

Dann bekomme ich folgende Lösungsmenge L:

\(L = \{ \begin{pmatrix} x_1\\x_2\\x_3\\x_4 \end{pmatrix} \in \mathbb{R}^4 | \begin{pmatrix} -14\\6\\0\\0 \end{pmatrix} + s*\begin{pmatrix} -8\\5\\1\\0 \end{pmatrix} + t*\begin{pmatrix} -12\\9\\0\\1 \end{pmatrix}, s,t \in \mathbb{R} \} \)

Frage:
Ich habe keine Lösungen dazu, ist dies die Parametrisierung nach der in der Aufgabenstellung gesucht ist ? 

Mein Lösungsweg:

 

Answer 1

Hallo

Deine Lösung hab ich nicht überprüft, das kannst du ja selbst durch einsetzen, Aber als Parameterlösung ist es richtig

Gruß lul

Comments

Ja ich habs zwei mal durchgerechnet, ein mal für mich und ein mal zum es hier posten. 
Da diese Aufgabe aber 8 Punkte gibt war ich mir nicht sicher ob ich irgendwas noch machen muss. Denn diese Anzahl Punkte erscheinen mir doch viel.