Unterschied beim Betrag

Question

Aufgabe:

|x|(x+2)

und

x(|x|+2)

Problem/Ansatz:

Wo ist der unterschied der beiden Funktionen.

Die Funktion |x|(x+2) verläuft wie ich es erwarte.

Doch den verlauf von x(|x|+2) verstehe ich nicht.

Wie berechnet man denn x(|x|+2)?

Comments

Wie berechnet man denn x(|x|+2)

Das ist ein sehr weites Feld, was willst du denn berechnen? Geht es dir darum, die Kurvenverläufe zu antizipieren?

Answer 1

Wie berechnet man denn x(|x|+2)?

x(|x|+2) = x*|x|+2x

für x≥0 ist das x^2 + 2x

und für x<0   -x^2 + 2x

Answer 2

Fallunterscheidung:

|x|(x+2)

1.Fall

x(x+2)=x^2+2x für x>=0

2.Fall:

-x(x+2) = -x^2-2x für x <0

x(|x|+2)

1. = x(x+2) = x^2+2x für x>=0

2. x(-x+2) = -x^2 +2x für x<0

Answer 3

Ich sehe 2 Terme.
Diese werden von dir als Funktionen bezeichnet.
Wie ist der Verlauf zu berechen.

Die Funktion |x|(x+2) verläuft wie ich es erwarte.

für x ≥ 0 gilt
x * ( x+ 2 ) = x^2 + 2x
für x < 0 gilt
-1 * x * ( x+ 2 ) = -x^2 -2

Doch den verlauf von x(|x|+2) verstehe ich nicht.
für x ≥ 0 gilt
x * ( x + 2 ) = x^2 + 2x
für x < 0 gilt
x * ( -1 *x + 2 ) = -x^2 + 2x

blau : erste Funktion
rot 2.Funktion

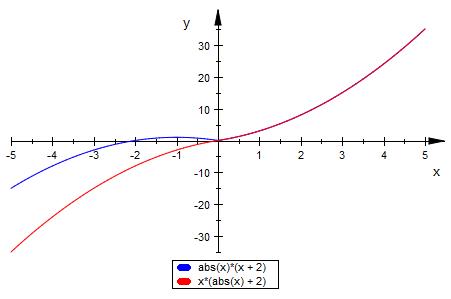
Für x >0 sind die Funktionen gleich.

Answer 4

Beide Kurven verlaufen für x>0 gleich.

Für die zweite Funktion f(x)=x(|x|+2) gilt f(-x)=-f(x). Daher muss der Graph punktsymmetrisch zum Ursprung verlaufen.

x	-2	-1	0	1	2
|x|(x+2)	0	1	0	3	8
x(|x|+2)	-8	-3	0	3	8