Rechnerisch:
Wenn alle Seitenlängen verdoppelt werden, bleiben die Winkel gleich groß; die Dreiecke sind ähnlich.
$$ A_1=a\cdot b\cdot \sin\gamma $$
$$ A_2=2a\cdot 2b\cdot \sin\gamma = 4\cdot a\cdot b\cdot \sin\gamma= 4\cdot A_1$$
Wenn du das zeichnest, siehst du, dass das kleine Dreieck viermal in das große Dreieck passt.
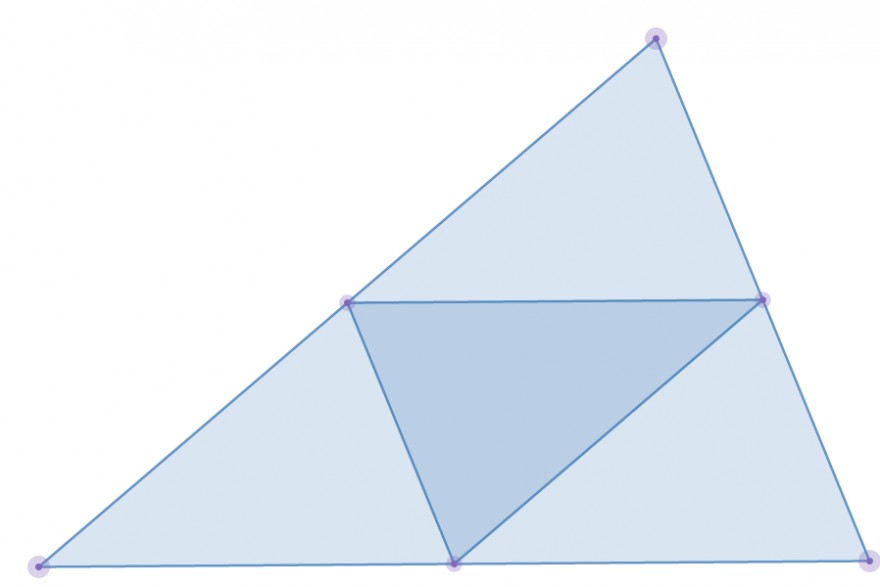
Nach deinem Kommentar sieht es so aus:

Jedes Teildreieck des großen Dreiecks ist so groß wie das ursprüngliche Dreieck. Zu jedem dieser Teildreiecke findet man eine gleiche Grundseite und Höhe im Vergleich mit einem anderen. Daher ist das große Dreieck 7mal so groß wie das zuerst gegebene.