Parabeln: Springbrunnen mit zwei entgegengesetzt gerichteten Wasserdüsen

Question

Ein Springbrunnen besitzt zwei entgegengesetzt gerichtete Wasserdüsen.Die Flugbahn des Wassers stellen Parabeln dar. Die Wasserdüsen sind 50cm über dem Wasser angebracht. Der Höhepunkt der Wasserflugbahn liegt bei 1,40m hoch und 60 cm von der Brunnenmitte entfernt.

a)Stelle die Funktionsgleichung auf (und zeichne den Graphen)

Answer 1

Setze den Scheitelpunkt auf die y-Achse. Dann weißt Du, dass der Punkt S(0|1,40) dabei sein muss.

Zudem weißt Du, dass die Parabel die Form y = ax^2+c haben muss (mit c = 1,40).

Es fehlt also ein weiterer Punkt um a zu bestimmen. Sei Dir bewusst, dass der Brunnen 60 cm vom Hochpunkt entfernt ist. Die Düsen sind dabei 0,5 m über dem Boden angebracht: P(-0,6|0,5).


Also

0,5 = a*(-0,6)^2 + 1,4   |-1,4

-0,9 = a*0,36   |:0,36

a = -2,5


--> y = -2,5x^2+1,4

 

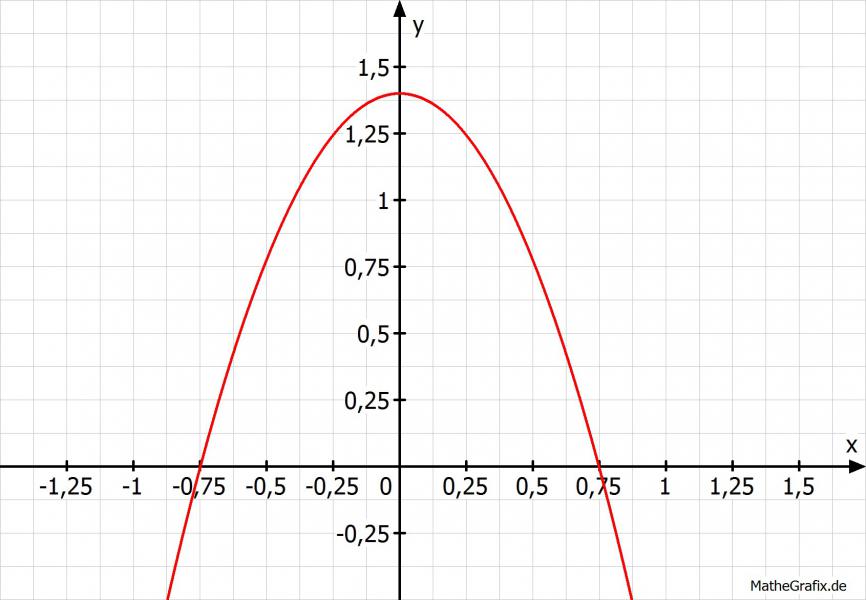
Beachte, dass der Brunnenmittelpunkt bei -0,6 zu finden ist.

 

Grüße

Comments

Das ist etwas anderst gemeint da steht ja 2 Düsen

Die fangen beide bei 0/0 an und die Brunnenmitte ist dann 60 cm entfernt.

---

Nun die zweite Düse musst Du einfach links von x = -0,6 anfügen. Es ist genau die gleiche Parabel, wie wir sie bereits haben.

Wo man den Mittelpunkt hinlegt ist egal, solange nicht anderweitig vorgegeben. So aber war die Bestimmung der Funktion besonders einfach ;).

---

ja der Mittelpunkt soll ja nicht bei der y-Achse liegen sondern  50 cm über dem Wasser und 60 cm neben der y achse bauf beisen seiten.(1,4m ist die größte Höhe )

---

Da steht nirgendwo, dass das nicht der Fall sein soll? ;)

Nun egal, wir haben ja die Parabel selbst schon bestimmt. Man muss sie nur noch verschieben. Ich empfehle die Scheitelpunktform. Diese ist ja y = a(x-d)^2+e mit S(d|e). Unser Scheitelpunkt ist ja S₁(0,6|1,4) bzw. S₂(-0,6|1,4). a ist bereits bekannt

y₁ = -2,5(x-0,6)^2+1,4

y₂ = -2,5(x+0,6)^2+1,4

 

Sieht dann so aus:

 

Alright? ;)

---

ja ,kann man die Gleichung auch anders angeben also nicht in scheitelform ?

---

Auch das kann man tun. Einfach ausmultiplizieren ;).

y₁ = -2,5(x-0,6)²+1,4 = -2,5(x^2-1,2x+0,36)+1,4 = -2,5x^2+3x+0,5

y₂ = -2,5(x+0,6)²+1,4 = -2,5x^2-3x+0,5

---

muss man nicht 1,4m -50 cm rechnen weil ja die drüsen 50 cm über dem boden sind ?

---

Jo, die Drüsen sind zwar 50cm über dem Boden, trotzdem trifft das Wasser letztlich den Boden ;).