Sinussatz: Wie breit ist der Fluss?

Question

Von zwei 250 m voneinander entfernt liegenden Punkten eines geraden Flussufers bilden das Ufer und die Peillinien nach einer Markierung am jenseitigen Ufer Winkel von 68, 87 Grad und 77, 45 Grad.  Wie breit ist der Fluss?

Hilfe erklärt mir das jm.

Comments

Bitte Text nochmals lesen. Stimmt das nun besser mit dem Original überein?

Wenn nicht: Als Kommentar bitte originalgetreue Fragestellung.

Answer 1

Hallo,

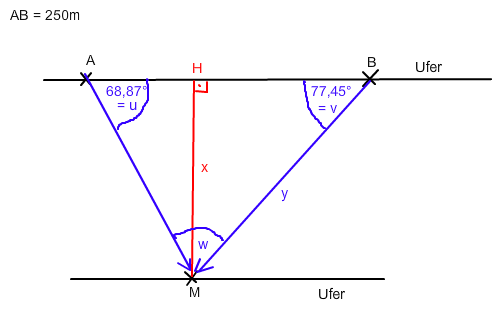
Winkel w = 180° - u - v  (Winkelsumme im Δ)

Im ΔABC gilt nach dem Sinussatz:  y / AB = sin(u) / sin(w)  →  y = sin(u)·AB / sin(w)    

Für die Flussbreite x gilt dann im rechtwinkligen Dreieck MBH :

tan(v) = Gegenkathete/Hypotenuse  = x / y  →   x = y · tan(v)    

Gruß Wolfgang

Comments

Analoger Kommentar wie der unter MCs Antwort möglich.

---

Scheint sich auf Antwort hier https://www.mathelounge.de/690915/sinussatz-ubungsaufgaben zu beziehen. Achtung: Andere Zahlen (gleicher Fragesteller). Fragwürdes Vorgehen: Geometrie ohne Skizzen der Fragestellen.

Bei "ähnlichen Fragen" sind teilweise noch Skizzen vorhanden. Bsp. https://www.mathelounge.de/150824/trigonometrie-flussbreite-bestimmen