Aufgabe:
Zwei Geländepunkte A und B werden von der Spitze eines 112 m hohen Turms in derselben Vertikalebene unter den Tiefenwinkeln α = 26,55° und β = 40° gesehen. Ermittle die Entfernung AB rechnerisch und graphisch.
Problem/Ansatz:
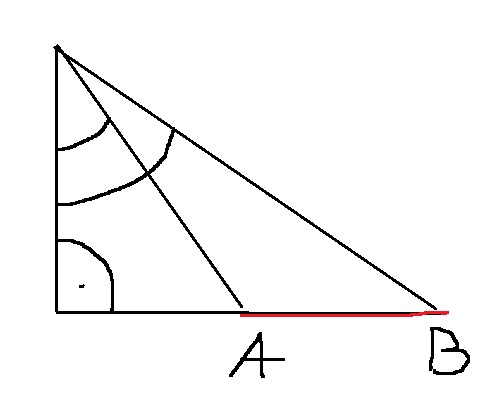
Hier meine Skizze mit Paint zur Aufgabe. Der kürze Winkel ist Alpha mit 26,55 Grad und der größere ist Beta mit 40 Grad ich muss nun die Rot gefärbte Strecke berechnen. Von der Aufgabenstellungher weiß ich das die linke Linie ja der Turm sein soll der insgesamt 112m hoch ist und somit auch ein rechter Winkel unten links in der Skizze entsteht. Allerdings weiß ich nicht wie ich das nun rechnen muss. Kann mir das jemand erklären?
Text erkannt:
\( A \)