Text erkannt:
14)
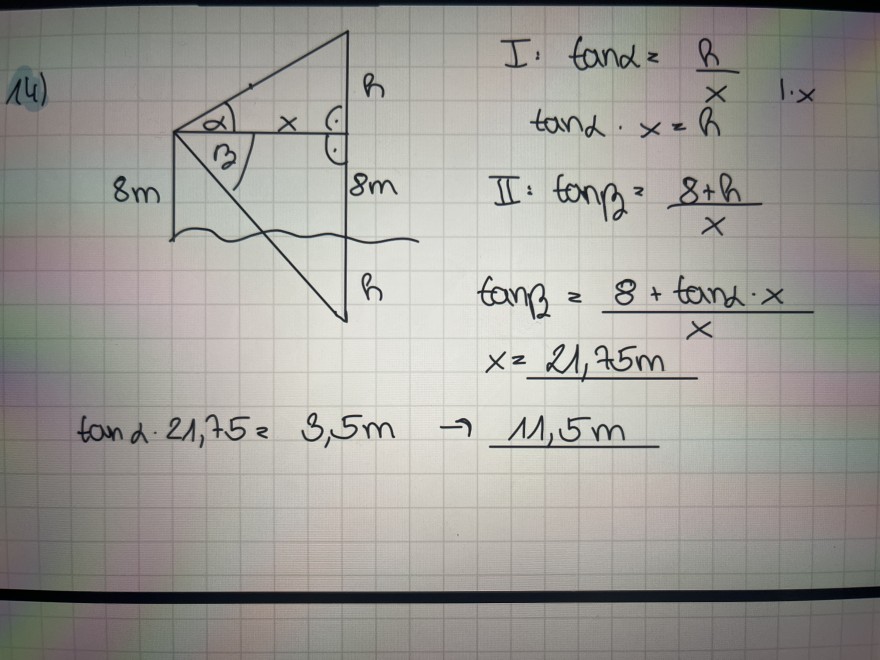
\( \begin{array}{l} \text { I. } \tan \alpha=\frac{h}{x} \text { I.x } \\ \tan \alpha \cdot x=h \\ \text { II: } \tan \beta=\frac{8+h}{x} \\ \tan \beta=\frac{8+\tan \alpha \cdot x}{x} \\ x=21,75 m \end{array} \)
\( \tan \alpha \cdot x=h^{x} \)
\( \tan \alpha \cdot 21,75=3,5 \mathrm{~m} \rightarrow 11,5 \mathrm{~m} \)
Aufgabe:
14) Fritz beobachtet von einem 8 m über dem Wasserspiegel befindlichen Fenster einen Hubschrauber unter einem Höhenwinkel von a = 37,9°, das Spiegelbild des Hubschraubers im Wasser unter einem Tiefenwinkel B = 48,9 °. Berechne die Flughöhe des Hubschraubers über dem Wasser.
Problem/Ansatz:
was habe ich falsch gemacht?