Kurvendiskussion mit einem Parameter: f(x):= (4x - t)/ x^2 , t > 0.

Question

Funktion: \( f(x)=\frac{4 x-t}{x^{2}} \quad, t \in ℝ, t>0 \)

a) Führen Sie eine Kurvendiskussion durch.

b) Zeichnen Sie den Graphen für t = 1, 2, 4.

c) Bestimmen Sie die Ortskurve der Extrema und Wendepunkte.

d) Bestimmen Sie für ein beliebigen Wert von t die Gleichung einer Wendenormalen

Answer 1

Kurvendiskussion: f(x) = (4·x - t)/x^2

Ableitungen (mind. zwei)

f(x) = (4·x - t)/x^2

f'(x) = 2·(t - 2·x)/x^3

f''(x) = 2·(4·x - 3·t)/x^4

Definitionsbereich

D = R \ {0}

Y-Achsenabschnitt f(0)

nicht definiert

Nullstellen f(x) = 0

4·x - t = 0

x = t/4

Extremstellen f'(x) = 0

t - 2·x = 0

x = t/2

f(t/2) = 4/t [für t > 0 ein HP]

f''(t/2) = - 32/t^3

Wendestellen f''(x) = 0

4·x - 3·t = 0

x = 3/4·t

f(3/4·t) = 32/(9·t)

Ortskurve der Extrempunkte

t - 2·x = 0

t = 2·x

y = (4·x - 2·x)/x^2 = 2/x

Ortskurve der Wendepunkte

4·x - 3·t = 0

t = 4/3·x

y = (4·x - 4/3·x)/x^2 = 8/(3·x)

Verhalten an den Rändern des Definitionsbereiches

lim (x → -∞) f(x) = 0-

lim (x → ∞) f(x) = 0+

lim (x → 0-) f(x) = -∞

lim (x → 0+) f(x) = ∞

Skizze

Comments

Vielen vielen Dank Coach :D.

Aber was ist denn mit Wendenormale gemeint? bzw. wie errechnet sich diese, wie ist der Wert.

---

Die Wendenormale geht durch den Wendepunkt und steht senkrecht auf der Wendetangente.

Ich nehme mal die Wendenormale für t = 1

Wendepunkt bei W(3/4; 32/9) 

f'(3/4) = -64/27

Wendenormale 

n(x) = 27/64 * (x - 3/4) + 32/9 = 27/64·x + 7463/2304

Answer 2

zu a) Eine Funktion f ( x ), deren Funktionsterm einen Parameter enthält (hier t), beschreibt eine Menge von "ähnlichen" Funktionen, die sich durch den Wert dieses Parameters unterscheiden.
Solch eine Menge von Funktionen nennt man auch "Funktionenschar" und bezeichnet diese unter Benutzung des Parameters mit f_t ( x )

Im Gegensatz zu den Ergebnissen einer Kurvendiskussion einer einzelnen Funktion  hängen die Ergebnisse einer Kurvendiskussion einer Funktionenschar im Allgemeinen von dem Parameter der Schar ab. Alle Extremstellen, Wendepunkt, Steigungen usw. werden also im Allgemeinen den Parameter t enthalten.

Als Beispiel führe ich die Bestimmung der Extremstellen vor:

Extremstellen von f_t ( x ) liegen höchstens an den Stellen x₀ vor, an denen gilt f_t ' ( x₀ ) = 0

Also: Bestimme f_t ' ( x ), setze f_t ' ( x ) = 0 und löse nach x auf:

f_t ( x ) = ( 4 x - t ) / x ²

Ableitung nach Quotientenregel (der Parameter t wird beim Ableiten als Konstante betrachtet):

f_t ' ( x ) = ( 4 * x ² - ( 4 x - t ) * 2 x ) / x ⁴

= ( 4 x ² - 8 x ² + 2 x t ) / x ⁴

= ( - 4 x ² + 2 x t ) / x ⁴

Nullsetzen:

( - 4 x ² + 2 x t ) / x ⁴ = 0

<=> - 4 x ² + 2 x t = 0

<=> x ( - 4 x + 2 t ) = 0

<=> x = 0 oder - 4 x + 2 t = 0

<=> x = 0 oder x = ( 1 / 2 ) t

Für x = 0 ist f_t ( x ) nicht definiert => keine Extremstelle.

Prüfung von x = ( 1 / 2 ) t durch Einsetzen in die zweite Ableitung von f_t ( x ):

f_t ' ' ( x ) = ( ( - 8 x + 2 t ) * x ⁴ - ( - 4 x ² + 2 x t ) * 4 x ³ ) / x ⁸

= ( - 8 x ⁵ + 2 t x ⁴ + 16 x ⁵ - 8 t x ⁴ ) / x ⁸

= ( 8 x ⁵ - 6 t x ⁴ ) / x ⁸

= ( 8 x - 6 t ) / x ⁴

Einsetzen von  x = ( 1 / 2 ) t:

( 8 * ( 1 / 2 ) t - 6 t ) < 0 => Maximum

An der Stelle x = ( 1 / 2 ) t liegt also ein Maximum der Funktionenschar f_t ( x ) vor. Wie man sieht, hängt die konkrete Extremstelle von dem konkreten Wert des Parameters t ab. Der Funktionswert f _t ( x = ( 1 / 2 ) t ) ist:

f _t ( x = ( 1 / 2 ) t ) = 4 ( 1 / 2 ) t - t ) / ( ( 1 / 2 ) t ) ² = t / ( t ² / 4 ) = 4 / t 

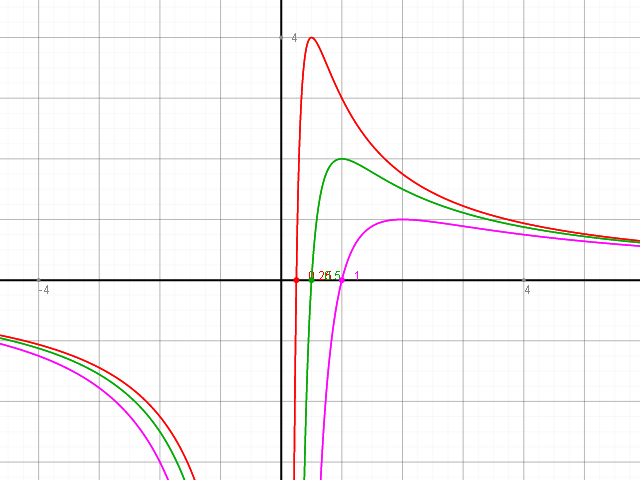
zu b) Im folgenden Bild sieht man die Funktionen f₁ ( x ) [rot] , f₂ ( x ) [ grün] und f₄ ( x ) [magenta] der Schar f_t ( x ). Man erkennt die Maxima und sieht, dass diese jeweils bei x = ( 1 / 2 ) t, also bei x = 1 / 2 bzw. x = 1 bzw. x = 2 liegen und verifiziert auch die Funktionswerte f_t ( ( 1 / 2 ) t ) = 4 / t für t = 1, 2 bzw. 4, also die Werte 4, 2 bzw. 1.

 

zu c) Die Ortskurve der Extrempunkte erhält man, indem man die Gleichung für die x-Koordinaten der Extrempunkte nach dem Parameter t auflöst und das Ergebnis in die Darstellung ihrer y-Koordinaten einsetzt. Also

x = ( 1 / 2 ) t

<=> t = 2 x

Einsetzen in die Gleichung für die y-Koordinaten der Extrempunkte:

y = 4 / t = 4 / ( 2 x ) = 2 / x

Hier ein Link zu WolframAlpha, wo noch einmal die drei Funktionen und zudem die Ortskurve (grün) der Extrempunkte dargestellt wird:

https://www.wolframalpha.com/input/?i=%284x-1%29%2Fx%C2%B2%2C%284x-2%29%2Fx%C2%B2%2C%284x-4%29%2Fx%C2%B2%2C2%2Fx+from+0to3

 

zu d) Wendestellen liegen höchstens dort vor, wo f_t ' ' ( x ) den Wert Null annnimmt, also:

f_t ' ' ( x ) = ( 8 x - 6 t ) / x ⁴ = 0

<=> 8 x = 6 t

<=> x = ( 3 / 4 ) t

Da ein beliebiger Wert von t gewählt werden soll, nehme ich den Wert t = 1 Die Wendestelle von  f₁ ( x ) ist somit:

x = 3 / 4

Um nun die Wendenormale bestimmen zu können, muss man zunächst die Steigung von f₁ ( x ) an der Stelle x = 3 / 4  bestimmen, also den Funktionswert von f₁ ' ( x ) an dieser Stelle bestimmen:

f₁ ' ( 3 / 4 ) = ( - 4 * ( 3 / 4 ) ² + 2 * ( 3 / 4 ) ) / ( 3 / 4 ) ⁴

= ( - ( 9 / 4 ) + ( 3 / 2 ) ) / ( 81 / 256 )

= ( - 3 / 4 ) * ( 256 / 81 )

= - 64 / 27

Da das Produkt der Steigungen einer Geraden und ihrer Normalen immer den Wert - 1 hat, kann man daraus nun die Steigung m_n der gesuchten Normalen bestimmen:

m_n = - 1 / ( - 64 / 27 ) = 27 / 64

Der Wendepunkt W ( x | f₁ ( x ) ) = ( ( 3 / 4 ) | 32 / 9 )  muss auf der Normalen liegen, also ist der y-Achsenabschnitt b_n der Normalen:

b_n = y - m_n * x = ( 32 / 9 ) - ( 27 / 64 ) * ( 3 / 4 ) = 7463 / 2304

Somit lautet die Gleichung der Wendenormalen an f₁ ( x ) :

y = ( 27 / 64 ) * x + 7463 / 2304

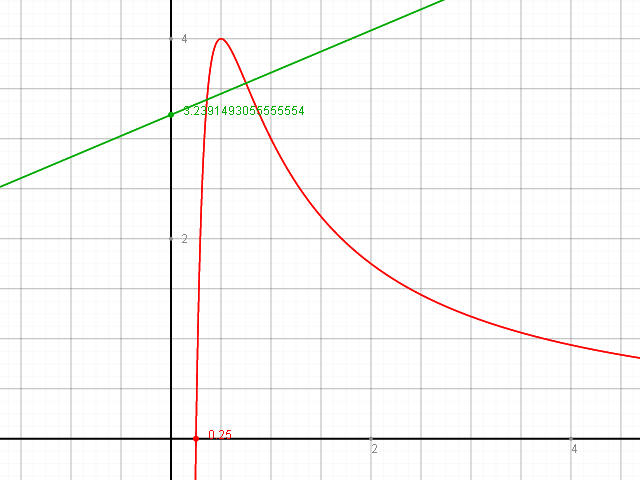
Hier ein Schaubild der Funktion f₁ ( x ) mit ihrer Wendenormalen: