Das Zehneck besteht aus 4 Quadraten und 8 gleichseitigen Dreiecken.
Die Rauten bestehen aus gleichseitigen Dreiecken, deren Seiten a genauso lang sind, wie die der Quadrate.
Die Formeln für die Flächeninhalte lauten: \(A_\square=a^2~~~;~~~A_\triangle=\frac{a^2}{4}\cdot\sqrt 3\)
Ziemlich langes Knobeln....
Jetzt habe ich die Lösung:
\(a\approx 1.855~~~;~~~A\approx 25.679 \,\text{FE}\)
Und so kommt man darauf:
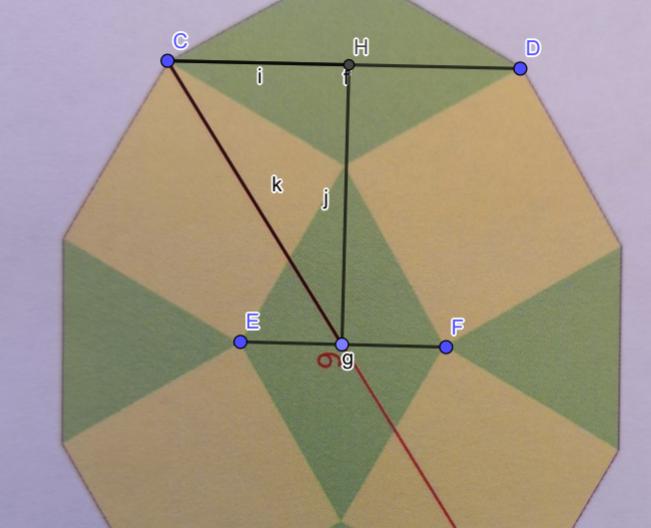
Mit Hilfe des Dreiecks aus i, j und k kann die Seitenlänge a bestimmt werden.
i ist die Höhe im gleichseitigen Dreieck \(\frac{a}{2}\sqrt 3\).
j ist die Höhe im gleichseitigen Dreieck plus die halbe Seitenlänge \(\frac{a}{2}\sqrt 3 +\frac{a}{2}\).
k=3.
Mit dem Satz des Pythagoras erhält man
$$ i^2+j^2=k^2 \Rightarrow \frac{3}{4}a^2 + \left(\frac{a}{2}\sqrt 3 +\frac{a}{2}\right)^2=9 \Rightarrow 3a^2+(a\sqrt 3 +a)^2=36$$
$$ 3a^2+ 3a^2 +2a^2\sqrt 3 +1a^2=36 \Rightarrow a^2\cdot(7+2\sqrt 3)=36$$
\(a=\dfrac{6}{\sqrt{7+2\cdot\sqrt 3}}\approx1.855\)
$$ A= 4A_\square+8A_\triangle=4a^2+8\cdot\frac{a^2}{4}\cdot\sqrt 3\approx 25.679 \,\text{FE}$$