Hallo,
Mache Dir zunächst eine Zeichnung. Zeichne in einem kartesischen Koordinatensysetm die drei Punkte \(P\), \(Q\) und \(R\) ein. Für den Vektor \(\vec{PQ}\) verbinde die Punkt \(P\) und \(Q\) mit einem Pfeil (blau), der bei \(P\) beginnt und bei \(Q\) endet.
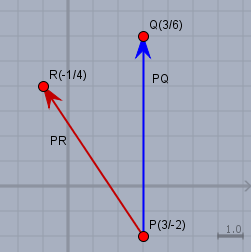
Genauso gehe für den Vektor \(\vec{PR}\) vor. Der Pfeil (rot) geht von \(P\) nach \(R\). Für die Berechnung so eines Vektors musst Du den Startpunkt (hier immer \(P\)) vom Zielpunkt subtrahieren. Man schreibt:$$\vec{PQ} = Q - P = \begin{pmatrix} 3\\ 6 \end{pmatrix} - \begin{pmatrix} 3\\ -2 \end{pmatrix} = \begin{pmatrix} 3 - 3\\ 6 - (-2) \end{pmatrix} = \begin{pmatrix} 0\\ 8 \end{pmatrix}$$Der Vektor \(\vec{PQ}\) ist also ein Vektor mit den Koordinaten \((0/8)\), d.h. er zeigt 8 Einheiten senkrecht nach oben, was auch der Zeichnung entspricht.
Für den zweiten Vektor mache das selbe - immer Ziel - Start:$$\vec{PR} = R - P = \begin{pmatrix} -1\\ 4 \end{pmatrix} - \begin{pmatrix} 3\\ -2 \end{pmatrix} = \begin{pmatrix} -1 - 3\\ 4 - (-2) \end{pmatrix} = \begin{pmatrix} -4\\ 6 \end{pmatrix}$$vom Punkt \(P\) aus, muss man also \(-4\) Einheiten in x-Richtung und \(6\) Einheiten in y-Richtung zurück legen, um zum Punkt \(R\) zu kommen. Überprüfe das in der Skizze oben.
Gruß Werner