wie muss ich hier vorgehen?

Question

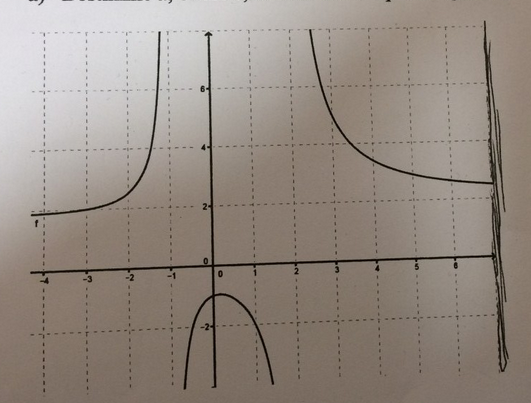
3.) Gegeben ist die Funktion \( f \) mit \( f(x)=\frac{a x^{2}+2}{(x+b)(x-c)} \)

a) Bestimme \( a, b \) und \( c, \) so dass der Graph zu \( f \) gehört:

b) Skizziere allgemein das Verfahren zur Bestimmung von waagrechten und senkrechten Asymptoten.
c) Beschreibe das Verhalten für grosse und kleine x und in der Umgebung von
Polstellen.

Answer 1

Die Polstellen kann m an ablesen. Es gilt \( b = 1 \) und \( c = 2 \)

Es gilt $$  \lim_{x\to\infty} f(x) = a $$

Aus dem Bild kann man ablesen das die Asymptote für \( x \to \infty \) 2 ist. Also ist \( a = 2 \)

Answer 2

Polstellen bei -b und c.

Asymptoten: y=a; x=-b; x=c