Funktionen berechenen

Question

Brauche Hilfe, komm mit dieser Nummer einfach nicht klar.

f(x)=2x^4-16x^2+14

Untersuchen Sie f(x) nach folgendem Schema

a) Symmetrieeigenschaften

b)Achsenschnittpunkte und Linarfaktordarstellung

c) Verhalten für x ±∞

d) Wertetabell und Graph


Vielen, vielen Dank schon mal vorrab.

Answer 1

a) Ich würde sagen dass die Funktion Achsensymmetrisch ist, da alle Exponenten gerade sind.

    Kann man auch mit f(x) = f(-x) beweisen.

    f(-x) = 2(-x)⁴-16(-x)²+14 = 2x⁴-16x²+14 = f(x), somit gilt f(x) = f(-x)
 

Answer 2

 

f(x) = 2x⁴ - 16x² + 14

 

a) Symmetrieeigenschaften

Wir sehen sofort, dass alle Exponenten gerade sind (4, 2 und 0). Deshalb ist die Funktion achsensymmetrisch zur y- Achse. Formale Überprüfung:

f(x) = 2x⁴ - 16x² + 14 =

f(-x) = 2(-x)⁴ - 16(-x)² + 14

 

b) Achsenschnittpunkte und Linearfaktordarstellung

Schnitte mit der x-Achse = Nullstellen

f(x) = 2x⁴ - 16x² + 14 | Substituieren x² = z

f(z) = 2z² - 16z + 14 | :2

z² - 8z + 7 = 0

z_1,2 = 4 ± √(16-7) = 4 ± 3

z₁ = 7

z₂ = 1

Die Nullstellen liegen also für f(x) bei

x₀ = √7

x₁ = -√7

x₂ = 1

x₃ = -1

Die Punkte lauten entsprechend (√7|0), (-√7|0), (1|0) und (-1|0)

Schnittpunkt mit der y-Achse:

x = 0 setzen, also f(0) = 14

Schnittpunkt (0|14)

Linearfaktordarstellung

f(x) = 2x⁴ - 16x² + 14

Wir haben die Nullstellen, können also schreiben:

f(x) = (x - √7) * (x + √7) * (x + 1) * (x - 1)

 

c) Verhalten für x -> ±∞

Dazu braucht man nur den Ausdruck mit dem höchsten Exponenten zu betrachten, also 2x⁴

Geht x -> +∞, so wird auch 2x⁴ unendlich groß.

Geht x -> -∞, so wird 2x⁴ ebenfalls unendlich groß.

 

d) Wertetabelle und Graph

Wertetabelle: Fleißarbeit, nichts für mich :-)

Graph:

 

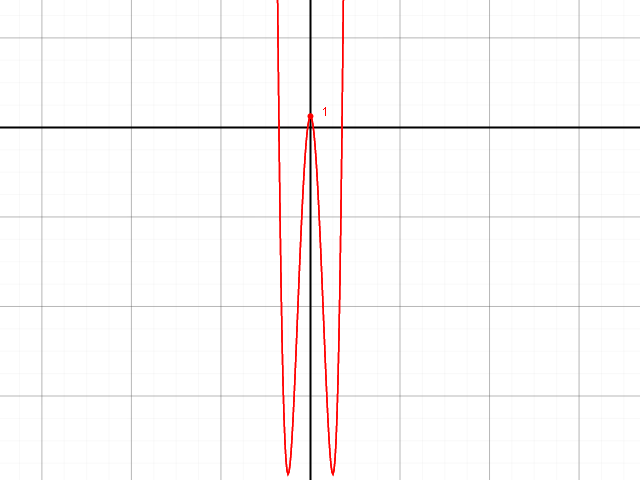
Besten Gruß

Comments

Vielen Dank schon mal, aber eine Frage habe ich noch bei welchen Werten muss ich den Graph nun zeichen?

---

Gern geschehen!

Das Zeichnen macht bei einer so steilen Funktion natürlich keinen rechten Spaß;

vielleicht kann man sich mit einem graphik-fähigen Taschenrechner oder dergleichen erst einmal einen groben Überblick über den Verlauf der Funktion verschaffen.

Ich würde nach Möglichkeit wichtige Punkte im Graphen zeigen: Nullstellen, Schnittpunkt mit y-Achse, nach Möglichkeit Extrema.

---

Ich mag Ihnen jetzt nicht sehr schlau  vorkommen, aber ich habe keine Ahnung wie man das macht.

---

Man tut Punkte machen in ein Koordinatensystem und dann tut man die Punkte verbinden.

---

Keine Sorge, wir lernen alle!

Man kann sich zum Beispiel eine Wertetabelle machen, indem man für x - sagen wir mal -

-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 einsetzt und für den dieser Werfte f(x) berechnet:

x         f(x)

-5      864

-4      270

-3        32

-2      -18

etc.

Welche x-Werte man nimmt, muss man halt ausprobieren; für diese Funktion sieht man beispielsweise, dass man (-5|864) sehr schlecht einzeichnen kann.

Für x könnte man ja auch Werte nehmen wie -1, -0,8, -0,6, ...

Da sind der Fantasie keine Grenzen gesetzt; der f(x)-Wert muss natürlich korrekt berechnet werden.

Zum Einzeichnen geht man vom Ursprung des Koordinatensystems (0|0) x Stellen nach rechts bei positivem x, und x Stellen nach links bei negativem x. Dann geht man f(x) Stellen nach oben bei positivem f(x) und f(x) Stellen nach unten bei negativem x. Diesen Punkt markiert man dann.

Macht man das mit mehreren Punkten, versucht man diese möglichst "sanft" zu verbinden.

Kleines Beispiel:

f(x) = x²

Ich habe berechnet

x = -2 | f(-2) = 4

x = -1 | f(-1) = 1

x = 0 | f(0) = 0

x = 1 | f(1) = 1

x = 2 | f(2) = 4

Ich habe diese Stellen (mit einem roten Kreuz) markiert und dann versucht, sie (durch die grüne Linie) zu verbinden; sieht natürlich furchtbar aus, da ich mit der Maus nicht zeichnen kann :-(

 

---

 Jetzt hab ich das zum ersten mal verstanden.