Untersuchung von ganzrationalen Funktionen f(x)= -0,5x^3+1,25x^2+x-0,75

Question

Brauch Hilfe,

Untersuche die Funktion

 

f(x)= -0,5x³+1,25x²+x-0,75

 

a) Symmetrieeigenschaften

b) Verlauf für x ±∞

c) Achsenschnittpunkte

d) Linearfaktordarstellung

e) Wertetabelle und graphische Darstellung

 

Vielen Dank schonmal.

Answer 1

Hi,

Was genau bereitet Dir denn Probleme?

Ich gebe Dir mal skizzenhaft eine Vergleichslösung. Da wos hängt frag nach ;).

 

Du meinst übrigens wahrscheinlich -0,5x³+1,25x²+x-0,75?

a) Keine erkennbare Symmetrie. Diese gibt es nur wenn die Exponenten alle gerade oder ungerade sind (zumindest die für uns relevante Symmetrie).

Alternativ über

f(-x) = f(x)

f(-x) = -f(x)

 

b)

x -> ∞           --> -∞

x -> -∞         --> ∞

 

c)

Schnittpunkt mit der y-Achse:

S(0|-0,75) (einfach f(0) = y bestimmen, bzw. den Achsenabschnitt ablesen)

 

Schnittpunkt mit der x-Achse:

Polynomdivision durch raten einer der Nullstellen:

N₁(1/2|0), N₂(-1|0) und N₃(3|0)

 

d)

f(x) = -0,5(x-1/2)(x+1)(x-3)

Vorfaktor von höchster Potenz berücksichtigen (-0,5 bei -0,5x³) und dann die Nullstellen dransetzen.

 

e)

Wertetabelle aufstellen

 

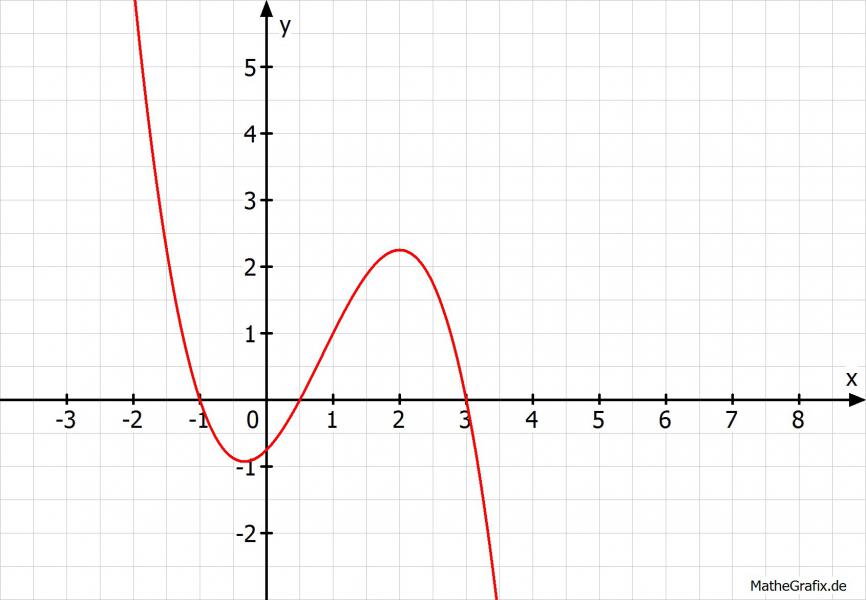
Grüße