Geraden und Geradenscharen im dreidimensionalen Raum

Question

Aufgabe:
Die Geraden g und h verlaufen durch die Kantenmittelpunkte des eingezeichneten Würfels.
Die Geradenschar ga geht durch die Punkte Q(0|0| 2) und P(2|2| a)
a) Überprüfen Sie, ob die Geraden g und
h in einer Ebene liegen.
b) Bestimmen Sie den Wert a, für welchen die Gerade g und die Gerade ga einen Schnittpunkt haben. Berechnen Sie dann die Koordinaten des Schnittpunktes.

Kann jemand schauen ob ich richtig gerechnet habe?

Comments

Kann jemand schauen ob ich richtig gerechnet habe?

Ich sehe keine Rechnung. Falsche Datei?

Answer 1

Hallo Julia,

Du hast Deine Lösung nicht gepostet. Hier mein Ergebnis zum Vergleich:

a) \(g\) und \(h\) sind weder parallel noch haben sie einen Schnittpunkt. Also liegen sie auch nicht in einer Ebene. Das folgende Bild zeigt das nochmal anschaulich

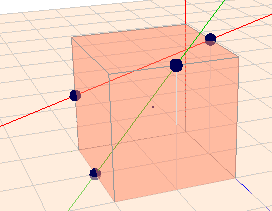
(klick auf das Bild, dann kannst Du die Szene mit der Maus drehen)

zu b) wenn man die beiden Geradengleichung gleich setzt erhält man $$s\begin{pmatrix} 2\\ 2\\ a-2 \end{pmatrix} + r \begin{pmatrix} -2\\1 \\ 1 \end{pmatrix} =  \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix} $$aus den ersten beiden Zeilen folgt \(r=s= \frac 13\) und die dritte Zeile $$\frac 13 (a-2) + \frac 13 = 0$$geht dann auf, wenn man \(a=1\) setzt. Folgende Szene zeigt das nochmal

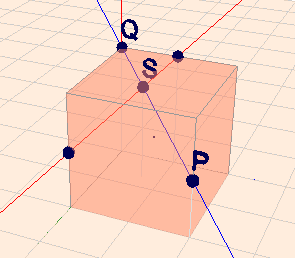
Die blaue Gerade ist \(g_{a=1}\). Der Schnittpunkt \(S\) liegt bei \(S=(2/3; \, 2/3;\, 5/3)\).

Gruß Werner

Comments

Oh ja habe ich vergessen, tut mir leid

Ich bekommen für a = 5 heraus

Aber finde meinen Fehler irgendwie nicht:

 

---

Für die 3. Gleichung hast du auf dem 1. Blatt noch richtig stehen

2 + at - 2t = 2 - r

(Das kann man verkürzen zu at - 2t = -r)

Auf dem 2. Blatt rechnest du jedoch mit

2t + at - 2t = 2 - r

---

Du hast die Zeile \(\text{III}\) einmal falsch abgeschrieben und ein \(t\) hinzu gemogelt.

$$ \text{III} \quad 2\colorbox{#ffff00}{t} + at - 2t = 2 -r $$

ganz oben auf der zweiten Seite. Das \(\colorbox{#ffff00}{t} \) ist zu viel.