Hallo alle zusammen, ich habe hier drei Aufgaben hier liegen. Ich habe sie probiert zu lösen und ich habe entsprechende Lösungen dabei. Nun bin Ich nur nicht sicher, ob sie richtig sind. Bitte korrigiert sie, falls nötig.
Aufgabe 1:
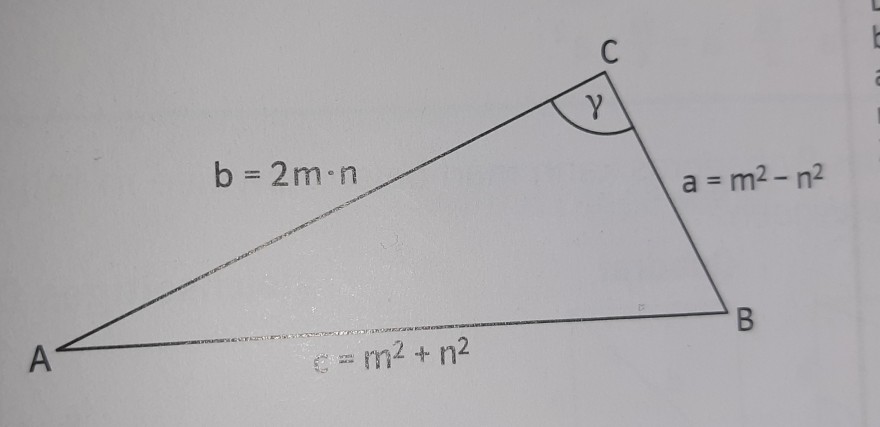
a) Die FIgur zeigt ein Dreieck mit den Seitenlängen a,b und c. Dabei stehen m und n für zwei positive natürliche Zahlen mit m > n. Wähle für m und n zwei beliebige Zahlen, berechne die Seitenlängen a,b und c und weise nach, dass Gamma = 90° ist.
b) Weise nach, dass das Dreieck für jede Wahl von m und n rechwinklg ist.
a) Ansatz:
(2m*n)^2 + (m^2-n^2)^2 = (m²+n²)²
<=>4m^2 * n² + m^4 -2m²n² + n² = m^4 + 2m²n² + n²
<=>4m²n² + m^4 - 2m²n² = m^4 + 2m²n²
<=>4m²n² - 2m²n² =2m²n²
<=>4m²n² = 2*(2m²n²)
=> Zahlen z.B. m = 4; n = 2
4*4²2² = 2(2*4²2²)
256 = 256
b) Ansatz: 4m²n² = 2*(2m²n²)
<=> 2 = 2
Aufgabe 2: In welcher Höhe über dem Erdboden befindet sich der Drachen, wenn der Junge seine Hand auf einer Höhe von 1,50m hält?
Ansatz:
25m + 1,5m = 26,5m Satz des Pythagoras:
20m + 1,5m = 21,5m a²+b²=c²
Berechnung:
(26,5)² - (21,5)² = a²
15,5m = a
Aufgabe 3: Die gegebene Aussage ist wahr. Gib die Umkehrung dieser Aussage in Wenn-dann-Formulierung an. Ist die Umkehrung dann auch gültig?
a) Wenn alpha = 20° und Beta = 30° ist, dann ist alpha+beta = 50°.
b) Wenn Fiffi ein Golden Retriever ist, dann ist er ein Hund.
c) Wenn eine Zahl durch 6 teilbar ist, dann ist sie durch 2 teilbar.
Ansatz:
a) Wenn alpha + Beta = 50° ist, dann muss alpha = 20° und Beta = 30° nicht sein, Z.B. alpha = 24°; Beta = 26°
b) Wenn Fiffi ein Hund ist, dann muss er nicht ein Golden Retriever sein. Z.B. Fiffi ist ein Labrador; ein Labrador ist ein Hund, aber nicht ein Golden Retriever.
c) Wenn eine Zahl durch 2 teilbar ist, dann ist sie nicht immer durch 6 teilbar.
Bsp: 2 : 2 = 1;
2 : 6 = 1/3 (Bruch)
Im Anhang findet man noch Fotos, die für den jeweiligen Aufgaben gegeben sind. 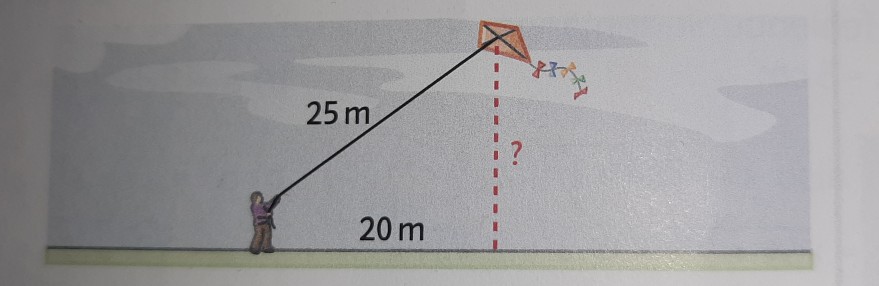
Text erkannt:
\( 25 \mathrm{m} \)
\( 20 \mathrm{m} \)
Text erkannt:
\( A \)
9