hi! ^^ :-)
u(t) = û sin( 2 π f t )
u(t) = û sin(ωt)
oben stehen zwei darstellungsformen der sinusspannung, einmal mit der frequenz f und darunter mit der kreisfrequenz ω = 2πf. in der kreisfrequenz ω steckt auch der von der zeit abhängige winkel φ(t) = ωt + φ0.
stichwort: zeigermodell https://de.wikipedia.org/wiki/Kreisfrequenz
in obiger aufgabe ist φ0 = 0. also gilt hier φ(t) = ωt.
u(t) = û sin(ωt)
12 = 73 sin(ωt) | hier der einfachheit halber ohne die einheit volt
sin(ωt) = 12/73
φ1 = ωt = arcsin(12/73) ≈ 0,165133 | wir müssen in rad rechnen, weil die kreisfrequenz in rad angegeben wird. das entspricht in etwa deinem berechneten winkel in grad.
t = φ/ω
t1 = 0,165133/(2π1200) ≈ 21,90144 * 10^{-6} s ≈ 21,9 μs.
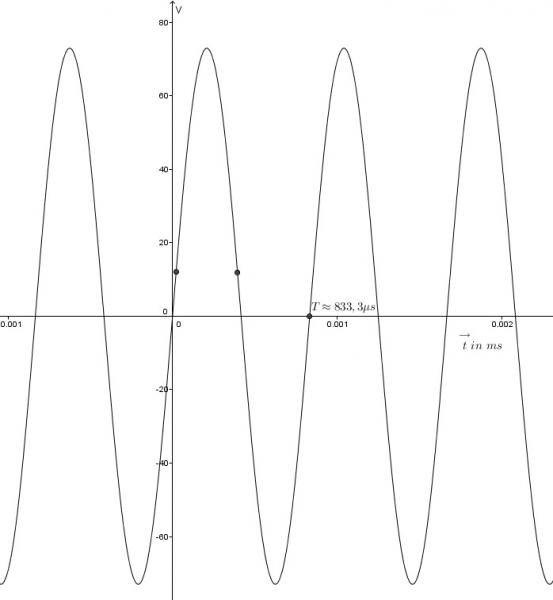
nach dieser zeit wird erstmalig der wert von 12V bei einem winkel von φ1 = 0,165133 erreicht.
weil der sinus periodisch ist, wird die spannung von 12V immer wieder erreicht. innerhalb einer periode zwei mal.
bei einer "normalen" sinusfunktion mit der periode 2π würde der y-wert
y = 12V an über dem winkel π - 0,165133 (in grad: 180° - 9.46°) erneut erreicht werden.
wie man oben sieht, ist π die hälfte von 2π, also die halbe periode bei der "normalen" sinusfunktion.
hier ist die periode aber nicht 2π sondern T = 1/f. also halbieren wir diese und
wir bekommen T/2 = 1/(2f) = 1/(2*1200) ≈ 4,167 * 10^{-4} s = 416,7 μs
jetzt können wir berechnen, wann das zweite mal 12V erreicht werden, das ist zum zeitpunkt
t2 = T/2 - t1
t2 = 416,7μs - 21,9 μs = 394,8 μs
der zugehörige winkel lässt sich mit φ2 = ω * t2 berechnen.
die 12V werte wiederholen sich während des schwingungvorgangs periodisch zu den zeitpunkten .
t1 + kT = t1 + 1/f und
t2 + kT = t2 + 1/f mit k ∈ ℤ
gruß
gorgar