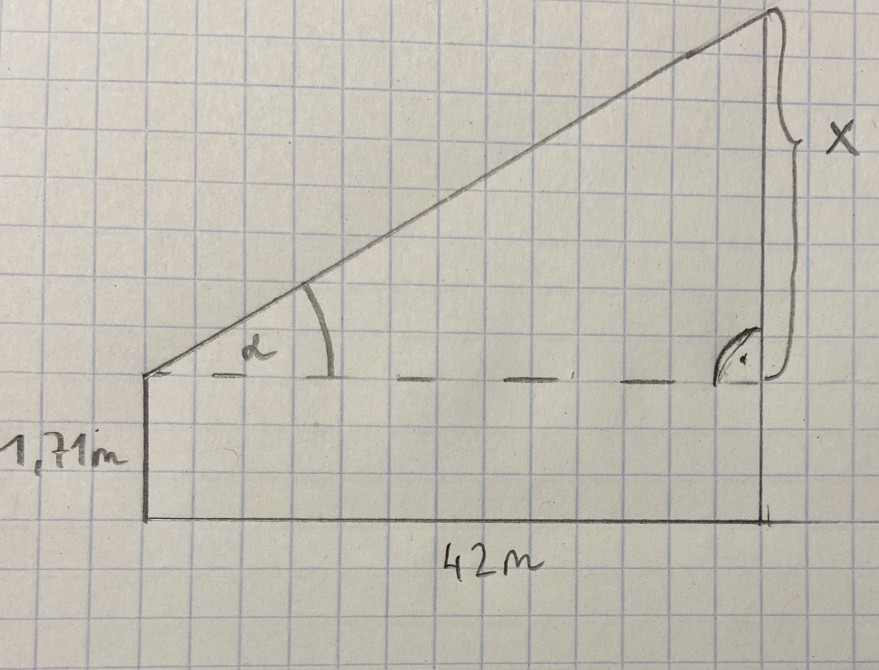
Zuerst berechnet man den ersten Teil der Baumhöhe, welche ich in einer selbst gezeichneten Skizze mit der Unbekannten x bezeichnet habe. Man weiß den Winkel α=45°, da es sich um ein gleichschenkelig, rechtwinkeliges Dreieck handelt. Zur Berechnung des x nimmt man die Formel tan(α)=G/A (G......Gegenkathete, A.....Ankathete). Diese Formel wandelt man auf G=tan(α)*A um. Also:
G=tan(45)*42 → G=68,030558m
Jetzt muss man noch den unteren Teil ausrechen, den der Baum hängt ja nicht in der Luft. Der untere Teil ist gleich hoch wie der Förster, nämlich 1,71m.
Daraus ergibt sich:
gesamte Baumhöhe= 68,03055+1,71≈69,741m Der Baum ist daher 69,741m hoch.