Hallo,
dazu kannst du ein Näherungsverfahren für die Nullstellen von f(x) = 1/ln(x) + ln(1/x) - ex benutzen, z.B. das
Newtonverfahren: [ f '(x) = - ex - 1/(x·LN(x)2) - 1/x ]
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel
\(x_{neu}=x_{alt}-\dfrac{f(x_{alt})}{f'(x_{alt})}\)
Infos dazu findest du hier:
https://de.wikipedia.org/wiki/Newton-Verfahren
mit den Startwerten x = 0,5 bzw. x =.1,5 ergibt sich z.B.:
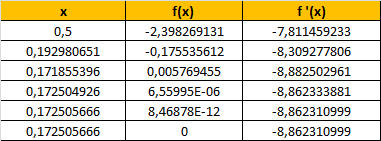
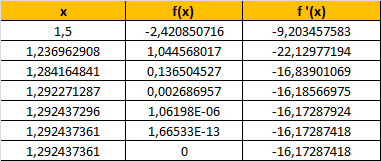
Gruß Wolfgang