Glasfläche auch mit Satz des Pythagoras berechnen

Question

Aufgabe:

Ein Spiegel mit angesetztem Rundbogen hat einen inneren Umfang von 6,9 m.

Berechne die Größe der Glasfläche.

Problem/Ansatz:

Wie kann ich diese Aufgabe lösen, indem ich unter anderem die Satzgruppe des Pythagoras (Satz des Pythagoras,Kathetensatz und Höhensatz) verwende.

Mir wurde außerdem als Hinweis gesagt, dass der Rundbogen am Spiegel KEIN Halbkreis ist.

In der beigefügten Skizze sollte alles zu erkennen sein.

Text erkannt:

\( \operatorname{riom} \)

Comments

Vom Duplikat:

Titel: Fläche mit Kreisbogen berechnen

Stichworte: kreisbogen,flächeninhalt

Aufgabe:

Ein Spiegel mit angesetztem Rundbogen hat einen inneren Umfang von 6,9 m.

Berechne die Größe der Glasfläche.

Problem/Ansatz:

Den Flächeninhalt des Rechtecks zu berechnen ist ja einfach. Aber wie kriege ich das mit dem Rundbogen hin?

Ich weiß dass der Rundbogen kein Halbkreis ist.

Breite des Spiegels: 1,20m

Höhe des Spiegels: 2,10m

Höhe des Kreisbogens: 0,40m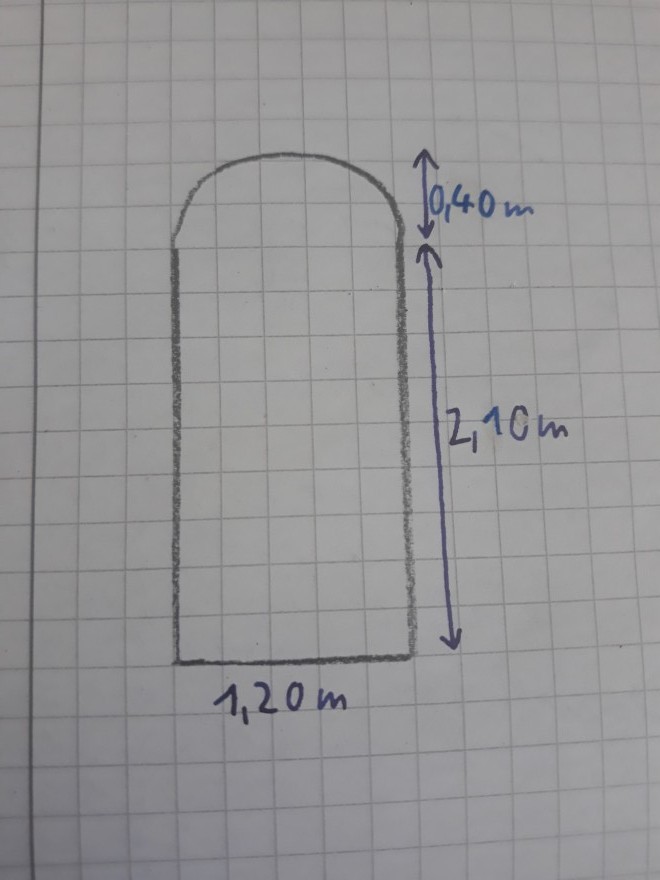

Text erkannt:

\( \underbrace{1}_{1,20 m} \)

---

"Ich weiß dass der Rundbogen kein Halbkreis ist."

und woher willst du das wissen ?

---

Hallo,

es handelt sich wohl um einen Korbbogen, dessen Konstruktion schon recht schwierig ist , zwischen  3 und 5 Mittelpunkten und Kreisen , schau bei geobra oder wiki wissen nach.

---

"es handelt sich wohl um einen Korbbogen"

WO zum Geier steht das in der Aufgabenstellung?!

---

es ist kein halbkreis. Steht im Aufgabenanhang

---

Gut, dass du den Anhang unerwähnt gelassen hast, so dass alle nicht sehen können, wie die Aufgabe exakt lautet.

So macht erklären und helfen richtig Spass!

---

Ich weiß,dass der Rundbogen kein Halbkreis und damit ist gut. Ich muss nicht erklären woher ich das weiß, wenn ich es als 100% sichere Tatsache mit dazu schreibe.

---

Der Rundbogen ist laut Wikipedia ein
HALBKREIS-Bogen. Siehe

https://de.wikipedia.org/wiki/Bogen_(Architektur)

---

Oder auch Dutzende weitere Varianten sind möglich, wenn der Kreisbogen von vorherein ausgeschlossen ist:

https://de.wikipedia.org/wiki/Bogen_(Architektur)#Halbkreisbogen_oder_Rundbogen

Damit ist die Grundlage genommen, die Frage korrekt zu beantworten.

Das ist dem Fragesteller egal - er bekommt ja trotzdem Antworten, auch wenn er sich weigert, die Voraussetzungen anzugeben.

Eigentlich ist das eine Schulung fürs Leben: Gib alle Informationen an, die dir zur Verfügung stehen, um eine gute Frage zu stellen, die zu einer guten Antwort führt.

Wer sich beharrlich weigert, auf Rückfragen einzugehen, verhindert damit den Lösungsweg zu verstehen.

Ist aber hier im Forum nicht wichtig - es gibt Antworten, weil es Punkte auf Antworten gibt.

Answer 1

Achtung: Sehr ungünstig ist jetzt, dass das Wort Kreisbogen gar nicht mehr in der Fragestellung auftaucht. Auch die Skizze des Lehrers (??) gibt dieses auch nicht sehr schön wieder.

Zu berechnen ist neben dem Rechteck ein Kreissegment/Kreisabschnitt

A = (1/2·ATAN(2·h/s)·(4·h^2 + s^2)^2 + h·s·(4·h^2 - s^2))/(16·h^2) = 0.3469

Erweitere das Kreissegment zu einem vollen Kreis. Dann kannst du das Kreissegment als Differenz eines Kreissektors und eines Dreiecks berechnen

(r - 0.4)^2 + 0.6^2 = r^2 → r = 0.65

tan(α/2) = 0.6/(0.65 - 0.4) → α = 134.76°

A = pi·0.65^2·134.76/360 - 1/2·1.2·(0.65 - 0.4) = 0.3469

Hier eine Skizze, damit du eine Idee bekommst

Comments

Hier mal der Vergleich der Modellierung über einen Kreisbogen und einer Ellipse.

Der Lehrer hat es irgendwie mehr wie eine Ellipse gezeichnet. Das verwirrt.

Ich habe es jetzt aber oben trotzdem mal wie ein Kreisbogen gerechnet.

---

Kannst du mir noch mal erklären wie genau ich das mit dem Satz des Pythagoras ausrechne? Das muss doch irgendwie möglich sein, ein Rundbogen, der kein Halbkreis ist mit der Satzgruppe des Pythagoras auszurechnen. Ich weiß der Flächeninhalt des Rundbogens ist ~0.32 m² aber ich brauche auch eine Rechnung dazu wie ich von dem Umfang(6,9m) und der Höhe(0,4m) des Rundbogens auf 0,32m² komme.

---

Rechnung steht oben

(r - 0.4)2 + 0.62 = r2 → r = 0.65

Das langt alleine noch nicht. Deswegen ist es etwas irreführend zu sagen man berechnet die Fläche mit dem Pythagoras. Der Pythagoras ist ein kleiner Winziger Schritt in der Rechnung.

---

und wie gehts dann weiter? ich habe jetzt den radius des kreisausschnitts.

---

Schau doch oben nach

Öffnungswinkel bestimmen

tan(α/2) = 0.6/(0.65 - 0.4) → α = 134.76°

Eine Skizze liegt extra dabei damit du sie dir nicht machen musst.

---

pi x 0.65·134.76/360 verstehe ich ja, aber was danach kommt leider nicht. könntest du mir das nochmal erklären?

---

Wenn man des Kreissektor berechnet ist das ja genau das Dreieck zuviel. Daher muss man dass Dreieck noch subtrahieren. Bitte einfach in die Skizze sehen.

---

achso Okay danke. ich fasse nochmal zusammen:

Ich rechne zuerst den radius aus:

(r - 0.4)2 + 0.62 = r2 → r = 0.65

dann den winkel:

0.6/(0.65 - 0.4) → α = 134.76°

dann kann ich den flächeninhalt ausrechnen:

A = pi·0.65 x 134.76/360 - 1/2·1.2·(0.65 - 0.4) = 0.3469m²

ja?

---

Genau.

Anderer Weg bei Wikipedia die Formel nachschlagen. Einsetzen. Ausrechnen. So wie ich es als erstes gemacht habe.

---

wie heißt die formel?

---

also welche meinst du?

---

vielen dank für die gute antwort. hatte die lösung zwar schon vor mehreren Tagen, aber hatte jetzt hab ich es gut verstanden, danke :)

Answer 2

Hallo,

es gib auch noch die Möglichkeit des gestelzten Rundbogen , dann  wäre die gesuchte Fläche ein Kreisegment, vorausgestzt der innere Umfang ist auch der äussere Umfang nach den Angaben

Bogenlänge  6,9 -2*2,1 -1,2 =1,5    , s=  1,2  ,    h = 0,4

dies alles in die Formeln zum Kreisabschnitt einfügen

                             https://www.matheretter.de/img/wiki/kreis-formeln.png

Comments

verstehe ich nicht wie das hilft?

---

Hallo, ,

die beste Anwort hat der Mathecoach gegeben. bezogen auf ein Kreissegment.

Die Formeln, die man dazu benötigt stehen in jeder guten Formelsammlung, vielleicht gelingt es damit Zusammenhänge zu der Aufgabe zu sehen.Leider ist es aus der ersten Fragestellung nicht ganz klar um welche Form von Bogen es sich handelt und / oder für welche Klassenstufe diese Aufgabe gedacht war, und was für einen Fragesteller absolut klar ist, ist für die Antwortgeber ein Rätsel.

---

ja ich habe es jetzt verstanden danke