Die Mathematik, die man in der Schule lernt, ist natürlich nicht die ganze Mathematik. Das kann auch gar nicht anders sein. Die Beschränkung auf Teilbereiche ist notwendig, weil die verfügbare Zeit begrenzt ist. Interessant und gleichzeitig bedauerlich ist, dass die Teile der Mathematik, welche in der Schule weggelassen werden, nicht selten diejenigen sind, die wirklich Spaß machen. Und vor wenigen Jahrzehnten waren noch Themen im Stoffplan, die geeignet waren, Spaß zu machen, die aber inzwischen herausgestrichen wurden. Ich denke da vor allem an die elementare Zahlentheorie.
Ian Stewart schreibt in seinem Buch „Mathematisches Sammelsurium“:
„Die Mathematik, die Sie nicht in der Schule gelernt haben, ist die eigentlich interessante.“
Zur elementaren Zahlentheorie bietet er insbesondere folgende Aufgabe an:
Beginnen Sie mit irgendeiner Zahl, sagen wir 471. Verlängern Sie diese Zahl durch sich selbst, also 471471. Dann teilen Sie durch 7, anschließen durch 11 und durch 13. Dann erhalten Sie genau die Zahl, mit der Sie gestartet sind.
Wen es jetzt nicht reizt, der Frage nachzugehen, ob das für alle dreistelligen Zahlen gilt, dem fehlt eine wichtige Grundvoraussetzung für das Lernen überhaupt. Die anschließende Frage: „Warum ist das so?“ bietet Anlässe, über elementare Fragen der Zahlentheorie nachzudenken.
Spiele mit mathematischem Hintergrund werden in der Schule ganz und gar vermieden. Es liegt nahe, zu vermuten, dass die Schulmathematik einem Prinzip folgt: „Mathematik darf keinen Spaß machen.“ Unter dem Link hier findet man ebenso Beispiele, wie bei Ian Stewart.
Einigen Zaubertricks – vor allem solchen, die mit Zahlen zu tun haben – liegt Mathematik zu Grunde. Man denke beispielsweise an all die verblüffenden Aufgaben, die mit den Worten „denke dir eine Zahl“ beginnen und am Schluss entweder die gedachte Zahl oder das errechnete Ergebnis nennen, das scheinbar von der gedachten Zahl abhängen müsste. Ein anderer Trick arbeitet mit folgendem Kartensatz:

Der Zauberer bittet einen Zuschauer, sich eine natürliche Zahl unter 32 zu denken und bei jeder Karte, die abgelegt wird zu sagen, ob die gedachte Zahl darauf ist oder nicht. Sofort danach nennt der der Zauberer die gedachte Zahl. Der Trick ist allerdings überzeugender, wenn der Kartensatz erweitert wird.
Die japanische Faltkunst ‚Origami‘ hat unzählige Bezüge zur Mathematik – vor allem zur Geometrie – findet aber im Mathematikunterricht nicht statt. Ein Beispiel findet man unter https://www.mathelounge.de/667485/kantenmodelle-platonischer-archimedischer-korper-origami
Auch Legespiele – wie einige Tangram – können Spaß machen und gleichzeitig zu mathematischen Entdeckungen Anlass geben. Ein Beispiel:
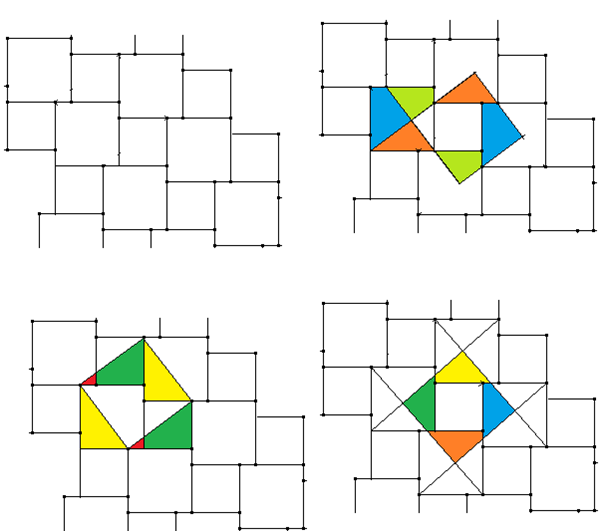
Im ersten Schritt werden Fliesen der Seitenlänge a und der Seitenlänge b im sogenannten „Römischen Verbund“ verlegt (erste Abbildung links oben unter diesem Absatz). Im zweiten Schritt wird eine Strecke in den Römischen Verbund gelegt, die Hypotenuse eines rechtwinkligen Dreiecks mit den Fliesenseiten a und b als Katheten ist. Im dritten Schritt wird diese Strecke als Seite eines Quadrats gewählt. Wenn jetzt das so gewonnene Quadrat die kleinere Fliese ganz enthält (rechts oben, rechts unten unter diesem Absatz) oder eine Ecke des neuen Quadrats auch Ecke der kleineren Fliese ist (unten links unter diesem Absatz), dann besteht das neue Quadrat aus 5 Teilen, mit denen man die beiden Fliesen auslegen kann.
Natürlich führen Zahlentheorie, Spiele, Zaubereien, Origami und Tangram zu mathematischen Themen, die nicht voraussetzungsfrei betrieben werden können. Aber genau dies könnte Schülerinnen und Schüler motivieren, den Dingen auf den Grund zu gehen.