Ermitteln sie, bei welcher Entfernung x der Sehwinkel φ am größten ist. Geben sie die Größe an.

Question

Aufgabe:

Das Völkerschlachtsdenkmal in Leibzig hat eine Gesamthöhe von 91m. Es besitzt in 69m Höhe 12 m hohe Wächterfiguren. Eine Beobachterin mit der Augenhöhe 1,6m steht x Meter vom Denkmal entfernt; ihr erscheinen die Figuren unter dem Sehwinkel φ.

Ermitteln sie, bei welcher Entfernung x der Sehwinkel φ am größten ist.

Geben sie die Größe des Sehwinkels in diese Fall an.

Comments

mach mal ne Skizze - ich kann grad nicht nach Leizig und mir das selber angucken.

Answer 1

Hallo,

Die Situation ist in etwa diese:

Die Strecke \(|OB| = (69-1,6) \text m\) und \(|BC| = 12 \text m\). Die Gesamtgröße spielt keine Rolle, da es nur um die Figuren geht. Der blaue Winkel in der Skizze sei \(\alpha\) und der grüne \(\varphi\) - der gesuchte Sehwinkel. Dann ist $$\tan \alpha = \frac{|OC|}x\\ \tan(\alpha - \varphi ) = \frac{|OB|}x \\ \tan{(\alpha - \varphi)} = \frac{\tan {\alpha} - \tan{\varphi}}{1+ \tan{\varphi} \tan{\alpha}} = \frac{|OB|}{x}$$Setze \(\tan \alpha\) in die letzte Gleichung ein und löse nach \(\tan\varphi\) auf$$\tan \varphi = \frac{x|BC|}{|OB|\cdot |OC| + x^2}$$Jetzt leite nach \(x\) ab (siehe dazu auch diese Antwort), setze die Ableitung zu 0 und löse nach \(x\) auf. Du erhältst$$x_{\text{opt}} = \sqrt{|OB| \cdot |OC|} = \sqrt{67,4 \cdot (67,4 + 12)} \, \text m \approx 73,2 \text m$$Der Sehwinkel \(\varphi\) beträgt in diesem Fall ca. \(4,7°\). Falls etwas unklar ist, so frage bitte nach.

Comments

Tan α ist doch (gegenkathethe / Ankathete).

währe das dann in dem Fall nicht (x/ |OC|) ?

---

OC liegt dem blauen Winkel GEGENÜBER, und x liegt AN ihm dran.

---

Tan α ist doch (gegenkathethe / Ankathete). Währe das dann in dem Fall nicht (x/ |OC|) ?

Im rechtwinkligen Dreieck \(\triangle AOC\) ist die Seite \(OC\) die Seite, die dem (blauen) Winkel \(\alpha\) gegenüberliegt. \(OC\) ist also die Gegenkathete. Die Seite \(AO = x\) liegt an dem Winkel \(\alpha\) (immer noch blau) - ist also die Ankathete.

Der Tangens ist Gegen- zu Ankathete (das ist richtig) - folglich $$\tan \alpha = \frac{|OC|}{x}$$

---

tanφ=x|BC||OB|⋅|OC|+x2

Und mir leuchtet nicht ganz ein, wie du das hier eingestzt hast, bzw. ich komme nicht mit dem x klar.

---

Vielen Dank, das mit den Katheten habe ich verstanden

---

tanφ=x|BC||OB|⋅|OC|+x2
Und mir leuchtet nicht ganz ein, wie du das hier eingestzt hast, bzw. ich komme nicht mit dem x klar.

Du hast$$\tan \alpha = \frac{|OC|}x\\  \frac{\tan {\alpha} - \tan{\varphi}}{1+ \tan{\varphi} \tan{\alpha}} = \frac{|OB|}{x}$$Das \(\tan \alpha\) von oben setze ich in die zweite Gleichung ein$$\begin{aligned} \frac{\frac{|OC|}x - \tan{\varphi}}{1+ \tan{\varphi} \frac{|OC|}x} &= \frac{|OB|}{x}\\    \frac{|OC|}x - \tan{\varphi} &= \frac{|OB|}{x} \left( 1+ \tan{\varphi} \frac{|OC|}x \right) \\     \frac{|OC|}x - \frac{|OB|}{x}  &= \frac{|OB| \cdot |OC|}{x^2}  \tan{\varphi} + \tan{\varphi} \\    \frac{|OC|}x - \frac{|OB|}{x}  &= \left( \frac{|OB| \cdot |OC|}{x^2}  + 1 \right) \tan{\varphi} \\    x( |OC| - |OB|)   &= \left( |OB| \cdot |OC|  + x^2 \right) \tan{\varphi}\\    x \cdot |BC|  &= \left( |OB| \cdot |OC|  + x^2 \right) \tan{\varphi}\\    \frac{x \cdot |BC| }{ |OB| \cdot |OC|  + x^2} &= \tan{\varphi} \end{aligned}$$

---

Hallo mardude,

sei doch bitte so nett und schreibe uns später wie der Lösungsweg Deines Lehrers aussieht - wenn Du ihn dann weist.

---

Besten Dank,

die Lösung, welche ich von meinem Lehrer erhalten habe, beinhalten lediglich:

\( \frac{12x}{x²+5351,56} \)

Answer 2

Versuch einer Lösung ohne Tangensfunktion:

Das Dreieck ABC besitzt einen Umkreis, in dem der Sehwinkel ein Peripheriewinkel gegenüber von BC ist.
Der Peripheriewinkel ist maximal, wenn der doppelt so große Zentriwinkel µ ebenfalls maximal ist. Dieser wiederum ist maximal, wenn M so nahe wie möglich an der y-Achse liegt.

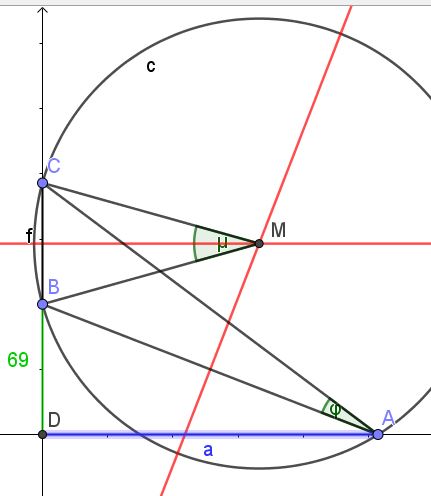
M ist der Schnittpunkt zweier Mittelsenkrechten des Dreiecks: Zum einen die waagerechte Gerade y=75, zum anderen die Mittelsenkrechte der Gerade AB.

Korrektur: Habe gerade nachträglich bemerkt, dass ich die Augenhöhe 1,6 m überlesen habe. Ich habe jetzt keine Zeit, die ganze Rechnung nochmal zu korrigieren, wichtig ist mir nur der alternative Weg. (Aus 69 müsste 67,4 werden, aus 75 entsprechend 73,4 mit allen weiteren Konsequenzen)

AB hat die Gleichung y=\( -\frac{69}{a}x+69 \) und den Mittelpunkt (0,5a | 34,5).
(Den Abstand musste ich hier mal mit "a" bezeichnen, weil ich x als Variable für Geradengleichungen benötige.)

Die Mittelsenkrechte von AB hat somit die Gleichung  y=\( \frac{a}{69}x+(34,5-\frac{a^2}{138} )\).

Im Schnittpunkt beider Geraden gilt

 \( 75=\frac{a}{69}x+(34,5-\frac{a^2}{138} )\)

\( \frac{a}{69}x=(40.5+\frac{a^2}{138} )\)

\( x=(\frac{40,5\cdot 69}{a} +\frac{a}{2})\)

Das wird minimal für a=74,56.

Für µ/2 gilt somit tan(µ/2)=\( \frac{6}{74,56} \),
(damit kommt der Tangens dann doch ins Spiel)

und  µ/2 ist sinnigerweise auch die Größe des gesuchten Peripherie-/Blick-Winkels.

Comments

Guter Ansatz! und wenn Du den jetzt weiter denkst, dann kommst Du nicht nur ohne Tangens sondern auch ohne Ableitung aus ;-)

---

Jetzt machst du mich neugierig.

Gut, das Minimum von x habe ich nur aus Bequemlichkeit mit Hilfsmitteln bestimmt, das geht sowieso ohne Ableitungen, die bei quadratischen Termen nicht erforderlich sind.

Aber der Übergang von einer Länge zu einem Winkel benötigt die Umkehrung einer Winkelfunktion; ohne Tangens dann eben mit Pythagoras und Sinus. Oder übersehe ich etwas Grundlegendes?

---

um final den konkreten Winkel zu berechnen, braucht man natürlich eine Winkelfunktion. Je nach Eingangsdaten kann das ja ein beliebiger Winkel sein.

Nein - ich meinte die Ableitung von \(x\) nach  \(a\). Und auch der Rechengang vorher lässt sich deutlich vereinfachen.

---

Und auch der Rechengang vorher lässt sich deutlich vereinfachen.

Möchtest du alle drei Punkte in die allgemeine Kreisgleichung einsetzen (unter Nutzung der bereits bekannten y-Koordinate des Mittelpunkts)?

---

Ich hatte diesen Kommentar schon vorher geschrieben - schicke ihn trotzdem noch ab :

WS meint wahrscheinlich, dass - wie du in deinem ersten Satz ausgeführt hast - a ohne Tangensfunktion bestimmt werden kann.

Nun sei der Kreismittelpunkt  M = (a | b) mit  b = (y2 + y1) / 2  =  (y(C) + y(B)) / 2 .

a wird jetzt dann minimal, wenn der Kreisradius r minimal wird, denn
a^2  =  r^2 - ((y2 - y1)/2)^2   und das wird er dann, wenn der Kreis die x-Achse berührt, also wenn r = b ist.

Man erhält also   a  =  √ (b^2 - ((y2 - y1)/2)^2 )  =  √ ( ((y2 + y1)/2)^2 - ((y2 - y1)/2)^2 )
=  √ (y2·y1)  =   √ (81·69)  =  74,76  
[ bzw.  mit Augenhöhen-Korrektur  a = √ (79,4·67,4) = 73,15  ]

und für den Winkel ergibt sich also genau dein
tan (φ) = tan (μ/2) = ( (y2 - y1)/2 )  /  ( (y2+y1)/2 )  =  (y2-y1) / (y2+y1)  =  12 / (81+69) = 0,08
[ bzw. mit Augenhöhen-Korrektur  tan (φ)  =  12 / (81-1,6 + 69-1,6)  =  0,0817 ]

---

a wird jetzt dann minimal, wenn der Kreisradius r minimal wird, ...  und das wird er dann, wenn er die x-Achse berührt, also wenn er gleich b ist.

Genial. Respekt an alle, die diese Idee hatten.

---

und das wird er dann, wenn der Kreis die x-Achse berührt

und damit ist die Hälfte des Weges zum Ziel zurück gelegt ;-) Jetzt noch ein genialer Gedanke und Ihr habt es.

Answer 3

Wenn f der Sehwinkel und a der Höhenwinkel bis zum Fuße der Figuren ist, dann

gilt  tan(a+f)=79,4 / x   und  tan(a ) = 67,4 / x

==>   f(x) = arctan(79,4/x) - arctan(67,4/x)

==>  f ' (x) = 67,4/(x^2 + 4542,76) - 79,4/(x^2 +6304,36)

also f ' (x) = 0 <=>  x= ±73,15 und der positive Wert ist der Gesuchte.

Answer 4

α(x) = ATAN((69 + 12 - 1.6)/x) - ATAN((69 - 1.6)/x)

α'(x) = 300·(133789 - 25·x^2)/((25·x^2 + 113569)·(25·x^2 + 157609)) = 0 --> x = 73.15

α(73.15) = 0.08184 = 4.689°

Skizze

~plot~ atan((69+12-1.6)/x)-atan((69-1.6)/x);[[0|300|0|0.1]] ~plot~

Völkerschlachtsdenkmal