Aufgabe:
Gegeben sei das Anfangswertproblem
$$ y^{\prime}(t)=t y(t), \quad y(0)=1 $$
mit der exakten Lösung \( y(t)=e^{\frac{t^{2}}{2}}, \) sowie ein zweistufiges, explizites Runge-Kutta Verfahren mittels des dazugehörigen Butcher-Schemas
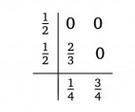
(a) Berechnen Sie zu dem gegebenen Anfangswertproblem die Verfahrensfunktion des Runge-Kutta-Verfahrens zum Butcher-Schema (3).
(b) Berechnen Sie damit eine Näherung an \( y(1) \) mit Schrittweite \( \frac{1}{2} \)
(c) Geben Sie den (globalen) Diskretisierungsfehler des Runge-Kutta-Verfahrens in \( t=1 \) an.
Problem/Ansatz:
Weiss jemand wie ich hier vorgehen muss bei der a)?