Ableitung von e^2x/ln√x

Question

Moin alle miteinander,

ich versuche die Ableitung von e^2x/ln√x zu finden.

Meine Rechnungen sehen so aus:

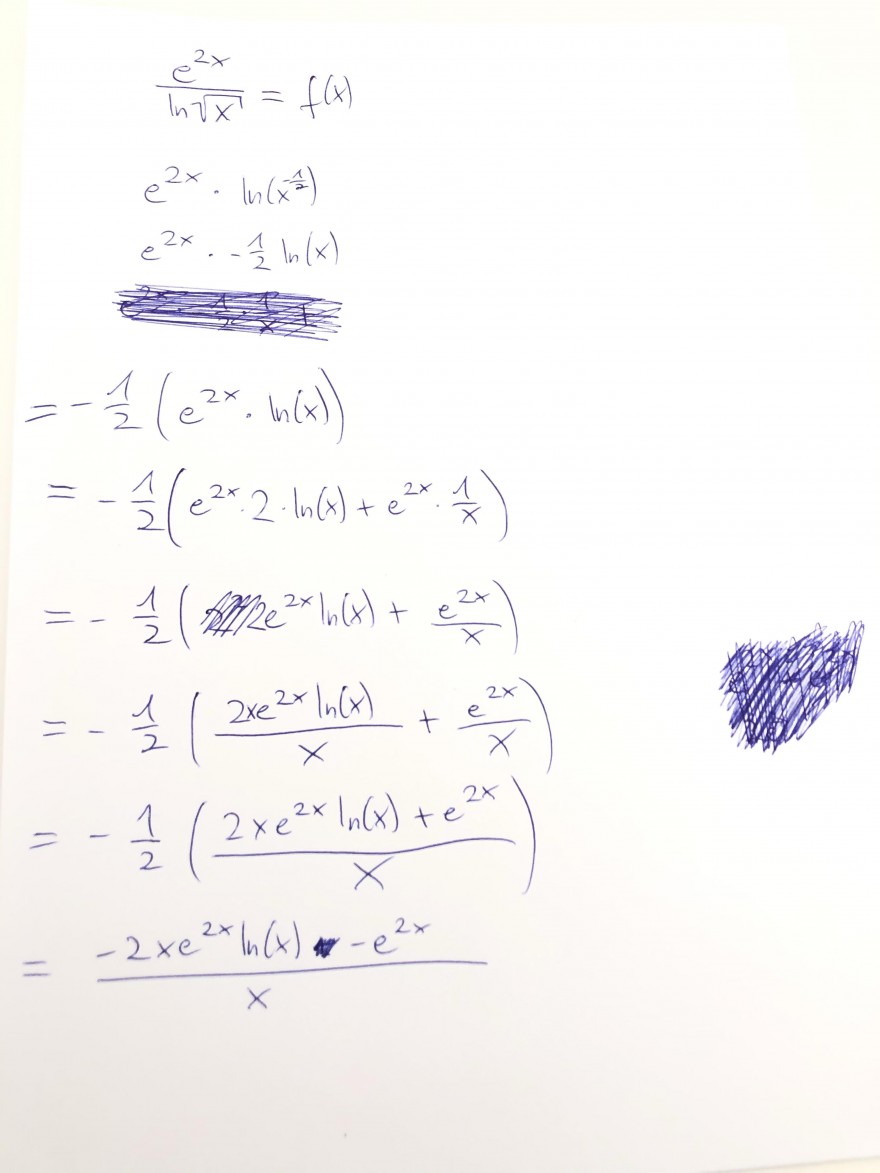
Text erkannt:

\( \begin{aligned} & \frac{e^{2 x}}{\ln \sqrt{x}}=f(x) \\ & e^{2 x} \cdot \ln \left(x^{\frac{1}{2}}\right) \\ & \frac{e^{2 x} \cdot-\frac{1}{2} \ln (x)}{x} \\=&-\frac{1}{2}\left(e^{2 x} \cdot \ln (x)\right) \\=&-\frac{1}{2}\left(e^{2 x} \cdot 2 \cdot \ln (x)+e^{2 x} \cdot \frac{1}{x}\right) \\=&-\frac{1}{2}\left(\sin x \ln 2 x \ln (x)+\frac{e^{2 x}}{x}\right) \\=&-\frac{1}{2}\left(\frac{2 x e^{2 x} \ln (x)}{x}+\frac{e^{2 x}}{x}\right) \\=&-\frac{1}{2}\left(\frac{2 x e^{2 x} \ln (x)+e^{2 x}}{x}\right) \\=&\left.\frac{-2 x e^{2 x} \ln (x)+e^{2 x}}{x}\right) \end{aligned} \)

Als Ergebnis steht bei mir jedoch etwas vollkommen anderes:

Text erkannt:

\( 05 . \mathrm{f}(\mathrm{x})=\frac{e^{2 x}}{\ln \sqrt{x}} \)
\( \mathrm{f}^{\prime}(\mathrm{x})=2 \mathrm{e}^{2 \mathrm{x} *} \frac{2 \ln x-\frac{1}{x}}{\ln ^{2} x} \)

 Kann mir jemand sagen, wo meine Fehler sind?

Liebe Grüße,

JaffaCake

Answer 1

Zum Vergleichen:

f '(x)=ê^2·x·(4/LN(x) - 2/(x·LN(x)^2))

Answer 2

Hallo,

der erste Schritt ist schon falsch $$\frac{e^{2 x}}{\ln \sqrt{x}} \ne e^{2x} \cdot \ln \left( x^{-\frac 12}\right)$$Richtig wäre$$\frac{e^{2 x}}{\ln \sqrt{x}} = e^{2x} \cdot \left( \ln\left( x^{+\frac 12}\right)\right)^{-1} = e^{2x} \cdot \left( \frac 12 \ln x\right)^{-1}$$Versuche es noch mal mit der Quotientenregel $$\begin{aligned} f(x) &= \frac{e^{2 x}}{\ln \sqrt{x}} \\ &= \frac{2e^{2x}}{\ln x} \\ f'(x) &= \dots\end{aligned}$$