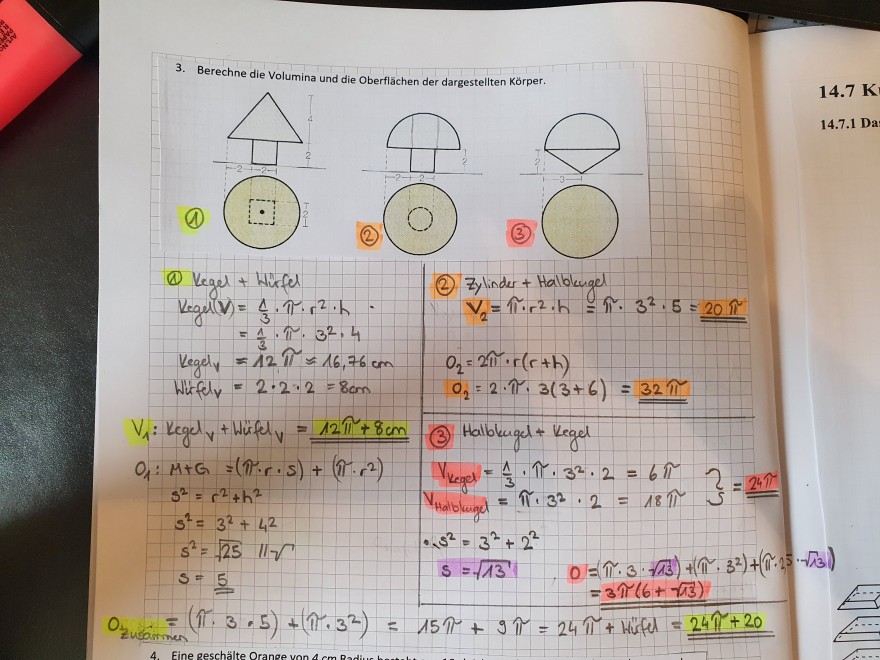
Text erkannt:
\( \theta(0) \)
Zylinder + Halblugel
\( V_{2}=\pi \cdot r^{2} \cdot h=\pi \cdot 3^{2} \cdot 5=\frac{20 \pi}{2} \)
\( \begin{array}{l}\text { Q kegel + Wirfel } \\ \begin{aligned} \operatorname{keg}(V) &=\frac{1}{3} \cdot \pi \cdot r^{2} \cdot h \\ &=\frac{1}{3} \cdot \pi \cdot 3^{2} \cdot 4 \\ &=12 \pi=16,76 \mathrm{cm} \end{aligned} & \begin{array}{l}\text { (2) }^{2} \\ \text { Which } y=2 \cdot 2 \cdot 2=8 \mathrm{cm}\end{array}\end{array} \)
\( 0_{2}=2 \cdot \pi \cdot 3(3+6)=32 \pi \)
\( V_{1}: k \cos \alpha_{v}+ \) Hisk \( \mu_{V}=12 \pi+8 \mathrm{cm} \quad \) (3) Halblugd \( + \) kegel
\( s^{2}=3^{2}+ \)
\( s^{2}=\sqrt{25} \| v \)
\( s=\frac{5}{\Rightarrow} \)\( \quad \begin{array}{cc}\cdot s^{2}=3^{2}+2^{2} & \\ s=\sqrt{13} & 0=\left(\pi \cdot 3 \cdot(\sqrt{3})+\left(\pi \cdot 3^{2}\right)+(\sqrt{1} \cdot 2 \cdot \sqrt{2} \cdot \sqrt{2})\right. \\ & =3 \pi(6+\sqrt{23})\end{array} \)
\( =(\pi \cdot 3 \cdot 5)+\left(\pi \cdot 3^{2}\right)=15 \pi+9 \pi=24 \pi+44 \mathrm{cta}=24 \pi+20 \)
KKann das jemand bitte überprüfen, ob ich richtig gerechnet habe