Question

Steckbriefaufgabe:

Der Graph einer Funktion 4. Grades ist symmetrisch zur y-Achse und hat in W(2|0) einen Wendepunkt. Der Anstieg der Wendetangente ist -8.

Answer 1

Aloha :)

Eine Funktion, die symmetrisch zur y-Achse ist, hat nur gerade Exponenten. Daher setzen wir an:$$f(x)=ax^4+bx^2+c$$$$f'(x)=4ax^3+2bx$$$$f''(x)=12ax^2+2b$$Bei \(x=2\) ist ein Wendepunkt, also muss \(f''(2)=0\) sein:$$0=f''(2)=48a+2b\quad\Rightarrow\quad b=-24a$$Der Anstieg der Wendetangente ist \(-8\), also ist \(f'(2)=-8\):$$-8=f'(2)=32a+4b=32a-96a=-64a\quad\Rightarrow\quad a=\frac{1}{8}\quad\Rightarrow\quad b=-3$$wir kurz den Zwischenstand zusammen:$$f(x)=\frac{1}{8}x^4-3x^2+c$$Nun nutzen wir noch den Punkt \((2|0)\) aus, d.h. \(f(2)=0\):$$0=f(2)=2-12+c=-10+c\quad\Rightarrow\quad c=10$$Damit haben wir das Ergebnis:$$f(x)=\frac{1}{8}x^4-3x^2+10$$

~plot~ x^4/8-3x^2+10 ; {2|0} ; -8(x-2) ; [[-8|8|-12|12]] ~plot~

Answer 2

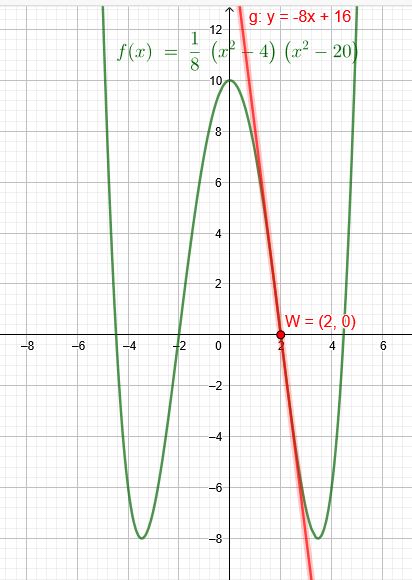
Der Graph einer Funktion 4. Grades ist symmetrisch zur y-Achse und hat in \(W_1(2|0)\) einen Wendepunkt. Der Anstieg der Wendetangente ist \(m=-8\)

Durch die Symmetrie zur y-Achse gilt auch  (W_2(-2|0)\)

\(f(x)=a(x-2)(x+2)(x-N)(x+N)\)

\(f(x)=a[(x^2-4)(x^2-N^2)]\)

\(m=-8\)

\(f'(x)=a[2x(x^2-N^2)+(x^2-4)(2x)]\)

\(f'(2)=a[4(4-N^2)+(4-4)(2x)]\)

\(f'(2)=4a[4-N^2]\)

\(4a[4-N^2]=-8\)  →  \(a[N^2-4]=2\) →  \(a=\frac{2}{N^2-4}\)

Wendepunkteigenschaft:

\(f'(x)=\frac{2}{N^2-4}[2x(x^2-N^2)+(x^2-4)(2x)  ]\)

\(f'(x)=\frac{2}{N^2-4}[2x^3-2xN^2+2x^3-8x ]\)

\(f'(x)=\frac{2}{N^2-4}[4x^3-2xN^2-8x ]\)

\(f''(x)=\frac{2}{N^2-4}[12x^2-2N^2-8  ]\)

\(f''(2)=\frac{2}{N^2-4}[48-2N^2-8 ]\)

\(\frac{2}{N^2-4}[48-2N^2-8 ]=0\)

\([40-2N^2 ]=0\)

\(N^2 =20\)   \(a=\frac{1}{8}\)

\(f(x)=\frac{1}{8}(x^2-4)(x^2-20)\)