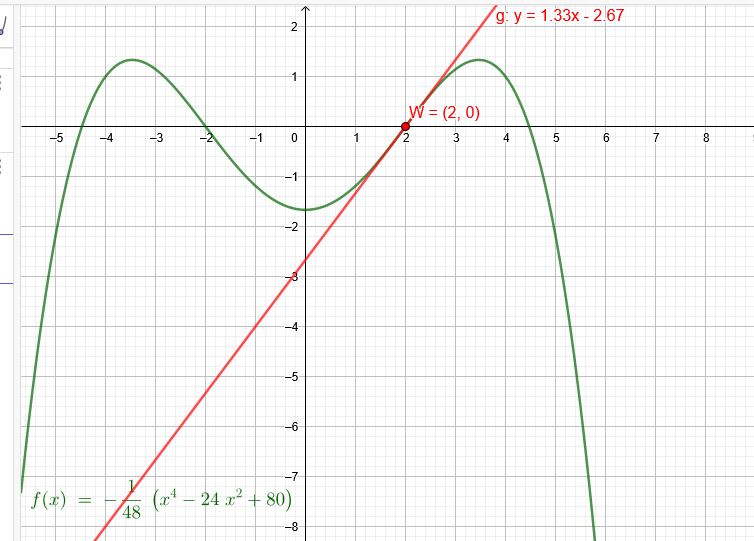
Bestimme sie eine ganzrationale Funktion 4.Grades deren Graph symmetrisch zur y-Achse ist und im Wendepunkt \(W(2|0)\) die Steigung \(m=\frac{4}{3}\) hat
symmetrisch zur y-Achse: \(W_1(2|0)\)→\(W_2(-2|0)\)
\(f(x)=a(x-2)(x+2)(x-N)(x+N)\)
\(f(x)=a[(x^2-4)(x^2-N^2)]=a[x^4-N^2x^2-4x^2+4N^2]\)
\(f'(x)=a[4x^3-2N^2x-8x]\)
\(f''(x)=a[12x^2-2N^2-8]\)
Wendepunkt:
\(f''(2)=a[48-2N^2-8]=a[40-2N^2]\)
\(a[40-2N^2]=0\)
\(N^2=20\)
Steigung \(m=\frac{4}{3}\)
\(f'(x)=a[4x^3-48x]\)
\(f'(2)=-64a=\frac{4}{3}\) \(a=-\frac{1}{48}\)
\(f(x)=-\frac{1}{48}[x^4-24x^2+80]\)