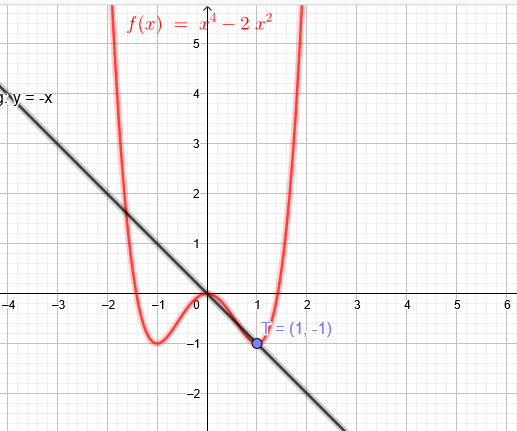
Bestimme rechnerisch eine ganzrationale Funktion f vierten Grades, deren Graph symmetrisch zur y-Achse verläuft und für die gilt: Im Ursprung hat der Graph eine waagerechte Tangente, an der Stelle x = 1 hat er einen Tiefpunkt, der auf der Geraden mit der Gleichung y = –x liegt.
Symmetrie zur y-Achse bedeutet:
\(f(x)=a*x^4+b*x^2+c\)
Graph geht durch den Ursprung:
\(f(0)=c\) \(c=0\)
Hat dort eine waagerechte Tangente:
\(f´(x)=4a*x^3+2b*x\)
\(f´(0)=0\)
an der Stelle x = 1 hat er einen Tiefpunkt, der auf der Geraden mit der Gleichung \(y = –x \) liegt: \(T(1|-1)\)
\(T(1|-1)\)
\(f(1)=a+b\) \(a+b=-1\)
\(f´(1)=4a+2b\) \(4a+2b=0\) \(2a+b=0\)
\(a=1 und b=-2\)
\(f(x)=x^4-2*x^2\)