Steckbriefaufgabe: ganzrationale Funktion vierten Grades, deren Graph achsensymmetrisch zur y-Achse verläuft, hat...

Question

Wie soll ich diese Aufgabe lösen?

Eine ganzrationale Funktion vierten Grades, deren Graph achsensymmetrisch zur Y-Achse verläuft, hat bei 2 eine Nullstelle. Der Graph von f hat im Punkt P (1|-6) die Steigung -2. Ermitteln sie den Funktionsterm. Wie soll ich diese Aufgabe lösen?

Answer 1

f(x) = ax^4+bx^2+c

f(2) = 0

f(1) = -6

f'(1) = -2

Answer 2

Eine ganzrationale Funktion vierten Grades,
f ( x ) = a*x^4 + b*x^3 + c * x^2 + d * x + e

deren Graph achsensymmetrisch zur Y-Achse verläuft,
( achsensymmetrie = nur gerade Exponenten
f ( x ) = a*x^4 + c * x^2 + e

hat bei 2 eine Nullstelle.
f ( 2 ) =  a*2^4 + c *2^2 + e = 0

Der Graph von f hat im Punkt P (1|-6) die Steigung -2.
f ( 1 ) = a + b + e = -6
f ´( x ) = 4*a*x^3 + 2 *c * x
f ´( 1 ) = 4*a + 2*c = -2

a*2^4 + c *2^2 + e = 0
a + b + e = -6
4*a + 2*c = -2

3 Gleichungen mit 3 Unbekannten.
Schaffst du das ?

Bin jetzt fernsehen.

mfg Georg

Answer 3

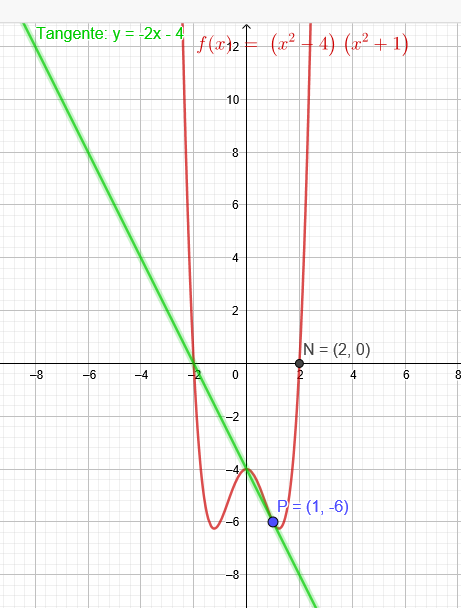
"Eine ganzrationale Funktion vierten Grades, deren Graph achsensymmetrisch zur Y-Achse verläuft, hat bei 2 eine Nullstelle. Der Graph von f hat im Punkt P (1|-6) die Steigung -2. Ermitteln sie den Funktionsterm."

bei 2 eine Nullstelle → bei -2 auch    Achsensymmetrie

\(f(x)=a*(x-2)*(x+2)*(x-N)*(x+N)\)

\(f(x)=a*[(x^2-4)*(x^2-N)]\)

\(P (1|-6)\):

\(f(x)=a*[(1^2-4)*(1^2-N)]=a*[3*(N-1)]\)

\(f(x)=a*[3*(N-1)]=-6→  a*(1-N)]=2\)→

\(a=\frac{2}{1-N}\)

\(f(x)=\frac{2}{1-N}*[(x^2-4)*(x^2-N)]\)

\(f´(x)=\frac{2}{1-N}*[2x*(x^2-N)+(x^2-4)*2x]\)

\(f´(x)=\frac{2}{1-N}*[2x*(2x^2-N-4)]\)

\(f´(1)=\frac{2}{1-N}*[2*(-2-N)]\)

\(\frac{2}{1-N}*[2*(-2-N)]=-2\)  →  \(\frac{1}{1-N}*[4+2N]=1\)

\(N=-1\)     \(a=1\)

\(f(x)=(x^2-4)*(x^2+1)\)