Komplexe Zahlen: Nullstellen des Polynoms: f(x) = 3x^3 + 3x^2 + 6

Question

Berechnen Sie alle Nullstellen des Polynoms:

f(x) = 3x^3  + 3x^2 + 6

ich kann diese Gleichung nicht lösen ,da es hier  kein  x^1 gibt,hat jemand eine Idee?

Answer 1

Nullstellen des Polynoms:

f(x) = 3x^3  + 3x^2 + 6

f(x) = 3 (x^3  + x^2 + 2) 

Hier kann nur die Klammer 0 sein. Wenn du diese Art von Aufgabe gestellt bekommst, weisst du, wie du allfällige Nullstelle(n) der Klammer finden (allenfalls erraten) kannst.

Answer 2

Du schreibst leider nicht, welche Klassenstufe, da sich an solchen Polynom-Aufgaben 500 Jahre Mathematik-Erkenntnisse wiederspiegeln:

a) 11. oder 12. Klasse (Wissenschaftler vor dem Jahre 1600): hier stellen Lehrer nur solche Aufgaben, wo:

- leicht geraten werden kann -> dann lautet die Aufgabe 3*x³-3*x²+6=0 (und Du hast Dich verschrieben)

- oder ein Näherungsverfahren angewendet werden soll (Bisektion, Newton Verfahren)

Für die 2 anderen Nullstellen kann man nach Polynomdivision die bekannte pq-Formel anwenden.

b) Schon kurz nach dem Jahre 1600 kannte man die https://de.wikipedia.org/wiki/Cardanische_Formeln

Diese hatten noch Fallunterscheidungen, die dann später mit Wurzeln & komplexen Zahlen zu einer PQRST-Formel optimiert wurde:

https://www.lamprechts.de/gerd/Bilder/QuadratischeGleichung_p-q-Formel_KubischeGleichung_PQRST-Formel.png

Unter

https://www.lamprechts.de/gerd/php/gleichung-6-grades.php 

werden beide Algorithmen mit Zwischenwegebnissen vorgerechnet:

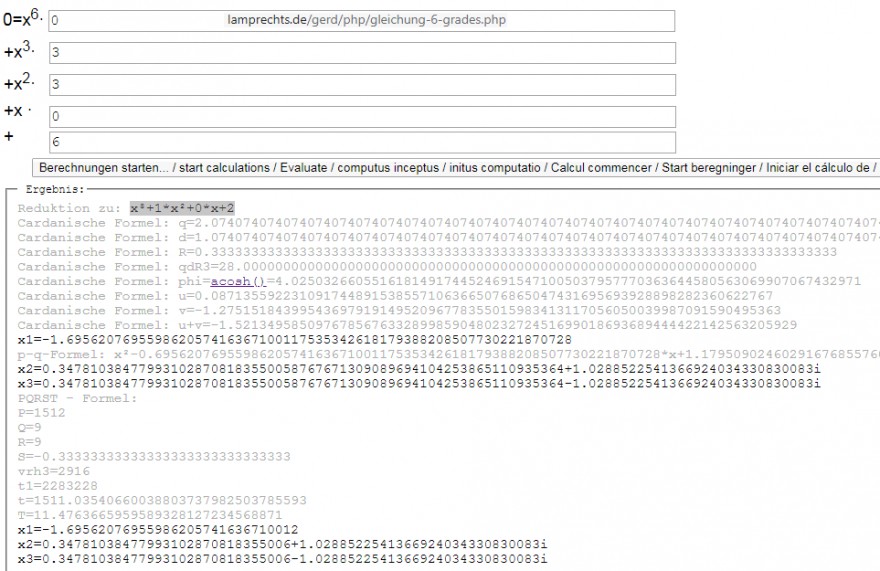
Für x₁ habe ich mal die explizite Formel herausgesucht & zusammengefasst, da sich dort die komplexen Anteile herauskürzen:

x₁ = (-1 - 1/(28 - 3 sqrt(87))^(1/3) - (28 - 3 sqrt(87))^(1/3))/3 = -1.69562076955986205741636710...

Hinweise:
sqrt(x)=Wurzel(x)
x^(1/3) = 3.Wurzel von x